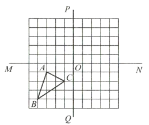
【题目】如图,在正方形网格当中,三角形![]() 的三个顶点都在格点上.直线
的三个顶点都在格点上.直线![]() 与直线
与直线![]() 相交于点
相交于点![]() .
.
(1)画出将三角形![]() 向右平移5个单位长度后的三角形
向右平移5个单位长度后的三角形![]() (点
(点![]() 的对应点分别是点
的对应点分别是点![]() ).
).
(2)画出三角形![]() 关于直线
关于直线![]() 对称的三角形
对称的三角形![]() (点
(点![]() 的对应点分别是点
的对应点分别是点![]() ).
).
(3)画出将三角形![]() 绕着点
绕着点![]() 旋转
旋转![]() 后的三角形
后的三角形![]() (点
(点![]() 的对应点分别是点
的对应点分别是点![]() ).
).
(4)在三角形![]() ,
,![]() ,
,![]() 中,三角形 与三角形 成轴对称,三角形 与三角形 成中心对称
中,三角形 与三角形 成轴对称,三角形 与三角形 成中心对称
参考答案:
【答案】(1)见解析;(2)见解析;(3)见解析;(4)![]() ,
,![]() ,
,![]() ,
,![]() .
.
【解析】
(1)将A、B、C分别向右平移5个单位,再顺次连接即可;
(2)分别找到A、B、C关于直线MN的对称点,再顺次连接;
(3)分别找到A、B、C关于O点的对称点,再顺次连接;
(4)观察图形,由轴对称和中心对称的定义进行判断.
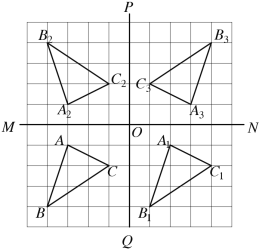
解:(1)如图所示,![]() 即为所求;
即为所求;
(2)如图所示,![]() 即为所求;
即为所求;
(3)如图所示,![]() 即为所求;
即为所求;
(4)由图形可知, ![]() 与
与![]() 成轴对称,
成轴对称,![]() 与
与![]() 成中心对称,
成中心对称,
故答案为:![]() ,
,![]() ,
,![]() ,
,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂计划生产480个零件.当生产任务完成一半时,停止生产进行反思和改进,用时20分钟.恢复生产后工作效率比原来可以提高20%,要求比原计划提前40分钟完成任务,那么反思改进后每小时需要生产多少个零件?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将边长为
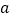 的正方形的边长增加
的正方形的边长增加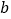 ,得到一个边长为
,得到一个边长为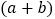 的正方形.在图1的基础上,某同学设计了一个解释验证
的正方形.在图1的基础上,某同学设计了一个解释验证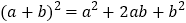 的方案(详见方案1)
的方案(详见方案1)
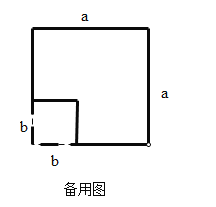
方案1.如图2,用两种不同的方式表示边长为
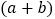 的正方形的面积.
的正方形的面积.方式1:
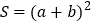
方式2:
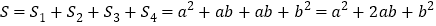
因此,
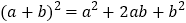
(1)请模仿方案1,在图1的基础上再设计一种方案,用以解释验证
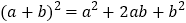 ;
;(2)如图3,在边长为
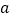 的正方形纸片上剪掉边长为
的正方形纸片上剪掉边长为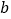 的正方形,请在此基础上再设计一个方案用以解释验证
的正方形,请在此基础上再设计一个方案用以解释验证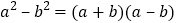 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如右图所示,图象过点(-1,0),对称轴为直线x=2,系列结论:(1)4a+b=0;(2)4a+c>2b;(3)5a+3c>0;(4)若点A(-2,y1),点B(,y2),点C(,y3)在该函数图象上,则y1<y3<y2;其中正确的结论有( )

A. 2个 B. 3个 C. 4个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】AD与BE是△ABC的角平分线,D,E分别在BC,AC上,若AD=AB,BE=BC,则∠C=( )

A. 69° B.
 C.
C.  D. 不能确定
D. 不能确定 -
科目: 来源: 题型:
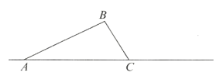
查看答案和解析>>【题目】如图,在三角形
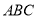 中,
中,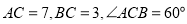 .将三角形
.将三角形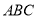 绕着点
绕着点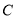 旋转,使得点
旋转,使得点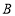 落在直线
落在直线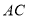 上的点
上的点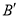 ,点
,点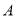 落在点
落在点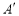 .
.
(1)画出旋转后的三角形
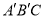 .
.(2)求线段
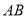 在旋转的过程中所扫过的面积(保留
在旋转的过程中所扫过的面积(保留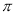 ).
).(3)如果在三角形
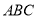 中,
中,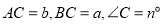 (其中
(其中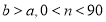 ).其他条件不变,请你用含有
).其他条件不变,请你用含有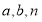 的代数式,直接写出线段
的代数式,直接写出线段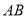 旋转的过程中所扫过的面积(保留
旋转的过程中所扫过的面积(保留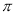 ).
). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,四边形ABCD是菱形,点M、N分别在AB、AD上,且BM=DN,MG∥AD,NF∥AB,点F、G分别在BC、CD上,MG与NF相交于点E;
(1)如图,求证:四边形AMEN是菱形;
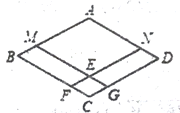
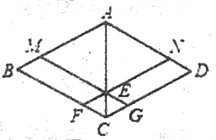
(2)如图,连接AC,在不添加任何辅助线的情况下,请直接写出面积相等的四边形;
相关试题

