【题目】已知,四边形ABCD是菱形,点M、N分别在AB、AD上,且BM=DN,MG∥AD,NF∥AB,点F、G分别在BC、CD上,MG与NF相交于点E;
(1)如图,求证:四边形AMEN是菱形;
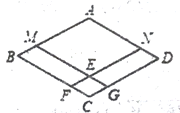
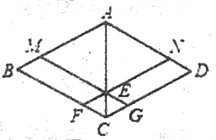
(2)如图,连接AC,在不添加任何辅助线的情况下,请直接写出面积相等的四边形;
参考答案:
【答案】(1)见解析;(2)S![]() =S
=S![]() ,S
,S![]() =S
=S![]() ,S
,S![]() =S
=S![]() ,S
,S![]() =S
=S![]() ,S
,S![]() =S
=S![]() .
.
【解析】
(1)由MG∥AD,NF∥AB,可证得四边形AMEN是平行四边形,又由四边形ABCD是菱形,BM=DN,可得AM=AN,即可证得四边形AMEN是菱形;
(2)易得四边形CGEF是菱形;即可得S![]() =S
=S![]() ,S
,S![]() =S
=S![]() ,S
,S![]() =S
=S![]() ,继而求得答案.
,继而求得答案.
(1)证明:∵MG∥AD,NF∥AB,
∴四边形AMEN是平行四边形,
∴四边形ABCD是菱形,
∴AB=AD,
∵BM=DN,
∴ABBM=ADDN,
∴AM=AN,
∴四边形AMEN是菱形;
(2)∵四边形AMEN是菱形,
∴S![]() =S
=S![]() ,
,
同理:四边形CGEF是菱形,
∴S![]() =S
=S![]() ,
,
∵四边形ABCD是菱形,
∴S![]() =S
=S![]() ,
,
∴S![]() =S
=S![]() ,S
,S![]() =S
=S![]() ,S
,S![]() =S
=S![]() ,S
,S![]() =S
=S![]() ,S
,S![]() =S
=S![]() .
.
-
科目: 来源: 题型:
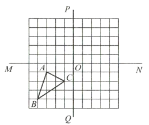
查看答案和解析>>【题目】如图,在正方形网格当中,三角形
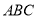 的三个顶点都在格点上.直线
的三个顶点都在格点上.直线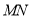 与直线
与直线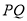 相交于点
相交于点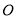 .
.
(1)画出将三角形
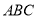 向右平移5个单位长度后的三角形
向右平移5个单位长度后的三角形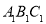 (点
(点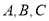 的对应点分别是点
的对应点分别是点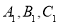 ).
).(2)画出三角形
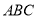 关于直线
关于直线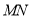 对称的三角形
对称的三角形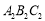 (点
(点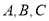 的对应点分别是点
的对应点分别是点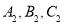 ).
).(3)画出将三角形
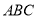 绕着点
绕着点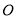 旋转
旋转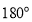 后的三角形
后的三角形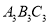 (点
(点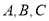 的对应点分别是点
的对应点分别是点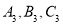 ).
).(4)在三角形
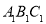 ,
,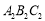 ,
,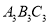 中,三角形 与三角形 成轴对称,三角形 与三角形 成中心对称
中,三角形 与三角形 成轴对称,三角形 与三角形 成中心对称 -
科目: 来源: 题型:
查看答案和解析>>【题目】AD与BE是△ABC的角平分线,D,E分别在BC,AC上,若AD=AB,BE=BC,则∠C=( )

A. 69° B.
 C.
C.  D. 不能确定
D. 不能确定 -
科目: 来源: 题型:
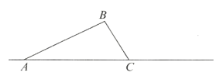
查看答案和解析>>【题目】如图,在三角形
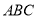 中,
中,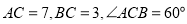 .将三角形
.将三角形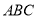 绕着点
绕着点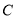 旋转,使得点
旋转,使得点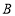 落在直线
落在直线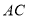 上的点
上的点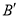 ,点
,点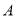 落在点
落在点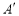 .
.
(1)画出旋转后的三角形
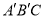 .
.(2)求线段
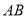 在旋转的过程中所扫过的面积(保留
在旋转的过程中所扫过的面积(保留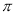 ).
).(3)如果在三角形
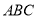 中,
中,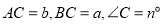 (其中
(其中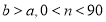 ).其他条件不变,请你用含有
).其他条件不变,请你用含有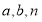 的代数式,直接写出线段
的代数式,直接写出线段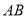 旋转的过程中所扫过的面积(保留
旋转的过程中所扫过的面积(保留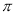 ).
). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),在Rt△ABC,∠ACB=90°,分别以AB、BC为一边向外作正方形ABFG、BCED,连结AD、CF,AD与CF交于点M;
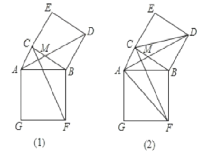
(1)求证:△ABD≌△FBC;
(2) 如图(2),已知AD=6,求四边形AFDC的面积;
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,BC=10,AB=
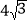 ,∠ABC=30°,点P在直线AC上,点P到直线AB的距离为1,则CP的长为_____.
,∠ABC=30°,点P在直线AC上,点P到直线AB的距离为1,则CP的长为_____. -
科目: 来源: 题型:
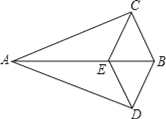
查看答案和解析>>【题目】如图,△ABC≌△ABD,点E在边AB上,CE∥BD,连接DE.
求证:(1)∠CEB=∠CBE;
(2)四边形BCED是菱形.
相关试题

