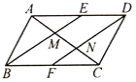
【题目】如图,在平行四边形ABCD中E、F分别是边AD、BC的中点,AC分别交BE、DF于点M、N,对于下列结论:①△ABE≌△CDF;②AM=MN=NC;③EM=![]() BM,④S△ABM=S△AME,其中正确的有( )
BM,④S△ABM=S△AME,其中正确的有( )
A.1个B.2个C.3个D.4个
参考答案:
【答案】C
【解析】
①已知四边形ABCD是平行四边形,可得AB=CD,AD=BC,∠DAB=∠DCB,已知E、F分别是边AD、BC的中点,可得AE=![]() AD=CF=
AD=CF=![]() BC,可证得△ABE≌△CDF
BC,可证得△ABE≌△CDF
②证明△ABM≌△CDN,得到AM=CN,再证明BE∥DF,F分别是边BC的中点,可得CN=MN,即可得出AM=CN=MN
③证明ME=![]() ND,因为△ABM≌△CDN,可得BM=DN,ME=
ND,因为△ABM≌△CDN,可得BM=DN,ME=![]() BM,可判断③
BM,可判断③
④在求△ABM和△AME面积时,有同一个高,它们的底分别为BM,ME,比较底边大小即可求解.
①∵四边形ABCD是平行四边形
∴AB=CD,AD=BC,∠DAB=∠DCB
∵E、F分别是边AD、BC的中点
∴AE=![]() AD=CF=
AD=CF=![]() BC
BC
∴△ABE≌△CDF
故①正确
②∵△ABE≌△CDF
∴∠ABM=∠NDC
∵四边形ABCD是平行四边形,AB∥CD
∴∠BAM=∠NCD,AB=CD
∴△ABM≌△CDN
∴AM=CN,
∵∠AEB=∠DFC
∵AD∥BC
∴∠AEB=∠EBC
∴∠DFC=∠EBC
∴BE∥DF
∵F是边BC的中点
∴CN=MN
即AM=CN=MN
故②正确
③∵BE∥DF,E是边AD的中点
∴M是边AN的中点,即ME是△AND的中位线
∴ME=![]() ND
ND
∵△ABM≌△CDN
∴BM=DN
∴ME=![]() BM
BM
故③正确
④过点A作AH⊥BE于H,如图所示
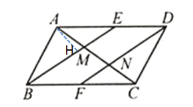
在求△ABM和△AME面积时,有同一个高AH,它们的底分别为BM,ME,
∵EM=![]() BM ,
BM ,
∴S△ABM>S△AME
故④错误
综上所述①②③正确
故选:C
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=
 x2﹣
x2﹣ x﹣9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.
x﹣9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.(1)求AB和OC的长;
(2)点E从点A出发,沿x轴向点B运动(点E与点A、B不重合),过点E作直线l平行BC,交AC于点D.设AE的长为m,△ADE的面积为s,求s关于m的函数关系式,并写出自变量m的取值范围;
(3)在(2)的条件下,连接CE,求△CDE面积的最大值;此时,求出以点E为圆心,与BC相切的圆的面积(结果保留π).

-
科目: 来源: 题型:
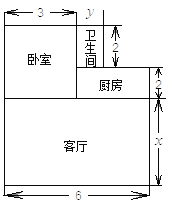
查看答案和解析>>【题目】小王购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示.根据图中的数据(单位:m),解答下列问题:
(1)用含
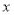 、
、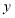 的代数式表示地面总面积;
的代数式表示地面总面积;(2)已知客厅面积比卫生间面积多21平方米,且地面总面积是卫生间面积的15倍.若铺1平方米地砖的平均费用为100元,那么铺地砖的总费用为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2013年四川南充3分)如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是【 】

A.12 B. 24 C. 12
 D. 16
D. 16
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,⊙O为△ABC 的内切圆,点D是斜边AB的中点,则tan∠ODA=_______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E,F,G,H分别是边AB,BC,CD,DA的中点.
(1)判断四边形EFGH的形状,并证明你的结论;
(2)当BD,AC满足什么条件时,四边形EFGH是正方形.(不要求证明)

-
科目: 来源: 题型:
查看答案和解析>>【题目】我市正在努力创建“全国文明城市”,为进一步营造“创文”氛围,我市某学校组织了一次“创文知识竞赛”,竞赛题共10题.竞赛活动结束后,学校团委随机抽查部分考生的考卷,对考生答题情况进行分析统计,发现所抽査的考卷中答对题量最少为6题,并且绘制了如下两幅不完整的统计图.请根据统计图提供的信息解答以下问题:
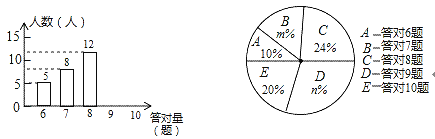
(1)本次抽查的样本容量是 ;
(2)在扇形统计图中,m= ,n= .
(3)补全条形统计图.
相关试题

