【题目】如图,E,F,G,H分别是边AB,BC,CD,DA的中点.
(1)判断四边形EFGH的形状,并证明你的结论;
(2)当BD,AC满足什么条件时,四边形EFGH是正方形.(不要求证明)

参考答案:
【答案】(1) 四边形EFGH是平行四边形,证明见解析;(2) 当BD=AC且BD⊥AC时,四边形EFGH是正方形.
【解析】试题分析:(1)、根据三角形中位线的性质得出EF∥HG,且EF=HG,从而得出平行四边形;(2)、要使邻边相等则需要满足BD=AC,要使有一个角为直角则需要满足BD⊥AC,从而得出正方形.
试题解析:(1)、四边形EFGH是平行四边形.
∵E,F分别是边AB、BC的中点,∴EF∥AC, 且EF=![]() AC
AC
同理:HG∥AC,且HG=![]() AC ∴EF∥HG,且EF=HG.∴四边形EFGH是平行四边形.
AC ∴EF∥HG,且EF=HG.∴四边形EFGH是平行四边形.
(2)、当BD=AC且BD⊥AC时,四边形EFGH是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】图1是由若干个小圆圈堆成的一个形如等边三角形的图案,最上面一层有一个圆圈,
以下各层均比上一层多一个圆圈,一共堆了n 层.将图1倒置后与原图1拼成图2的形状,这样我们可以
算出图1中所有圆圈的个数为1+2+3+…+n=
 .
.
如果图中的圆圈共有13层,请解决下列问题:
(1)我们自上往下,在每个圆圈中按图3的方式填上一串连续的正整数1,2,3,4,……,则最底层最左
边这个圆圈中的数是 ;
(2)我们自上往下,在每个圆圈中按图4的方式填上一串连续的整数-23,-22,-21,-20,……,求
最底层最右边圆圈内的数是_______;
(3)求图4中所有圆圈中各数的绝对值之和.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,∠A=60°,AC=a,作斜边AB边中线CD,得到第一个三角形ACD;DE⊥BC于点E,作Rt△BDE斜边DB上中线EF,得到第二个三角形DEF;依此作下去…则第n个三角形的面积等于 .
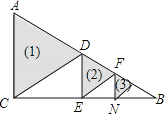
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点G、E、F分别在平行四边形ABCD的边AD、DC和BC上,DG=DC,CE=CF,点P是射线GC上一点,连接FP,EP,求证:FP=EP.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某河的两岸PQ、MN互相平行,河岸PQ上的点A处和点B处各有一棵大树,AB=30米,某人在河岸MN上选一点C,AC⊥MN,在直线MN上从点C前进一段路程到达点D,测得∠ADC=30°,∠BDC=60°,求这条河的宽度.(
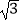 ≈1.732,结果保留三个有效数字).
≈1.732,结果保留三个有效数字).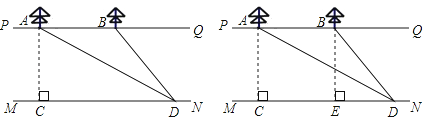
-
科目: 来源: 题型:
查看答案和解析>>【题目】现有两个不透明的乒乓球盒,甲盒中装有1个白球和2个红球,乙盒中装有2个白球和若干个红球,这些小球除颜色不同外,其余均相同.若从乙盒中随机摸出一个球,摸到红球的概率为
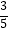 .
.
(1)求乙盒中红球的个数;
(2)若先从甲盒中随机摸出一个球,再从乙盒中随机摸出一个球,请用树形图或列表法求两次摸到不同颜色的球的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是一个菱形绿地,其周长为40
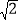 m,∠ABC=120°,在其内部有一个四边形花坛EFGH,其四个顶点恰好在菱形ABCD各边的中点,现在准备在花坛中种植茉莉花,其单价为10元/m2,请问需投资金多少元?(结果保留整数)
m,∠ABC=120°,在其内部有一个四边形花坛EFGH,其四个顶点恰好在菱形ABCD各边的中点,现在准备在花坛中种植茉莉花,其单价为10元/m2,请问需投资金多少元?(结果保留整数)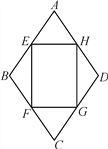
相关试题

