【题目】如图,已知AB∥EF,∠C=90°,∠B,∠D,∠E三个角的大小分别是x,y,z则x,y,z之间满足的关系式是( )
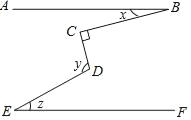
A. x+z=yB. x+y+═180°C. x+y﹣z=90°D. y+z﹣x=180°
参考答案:
【答案】C
【解析】
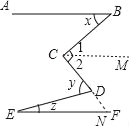
先过C作CM∥AB,延长CD交EF于N,得到∠CNE=y﹣z,再根据CM∥AB∥EF,
得到∠ABC=x=∠1,∠2=∠CNE,∠1+∠2=90°,即可解答
过C作CM∥AB,延长CD交EF于N,则∠CDE=∠E+∠CNE,即∠CNE=y﹣z
∵CM∥AB,AB∥EF,
∴CM∥AB∥EF,
∴∠ABC=x=∠1,∠2=∠CNE,
∵∠BCD=90°,
∴∠1+∠2=90°,
∴x+y﹣z=90°.
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,任意一个正整数
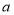 都可以进行这样的分解:
都可以进行这样的分解: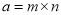 (
(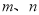 是正整数,且
是正整数,且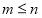 ),在
),在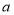 的所有这种分解中,如果
的所有这种分解中,如果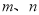 两因数之差的绝对值最小,我们就称
两因数之差的绝对值最小,我们就称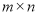 是
是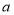 的最佳分解并规定:
的最佳分解并规定: ,例如:12可以分解成1×12、2×6、3×4,因为:
,例如:12可以分解成1×12、2×6、3×4,因为: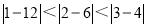 ,所以3×4是12的最佳分解,所以F(12)=
,所以3×4是12的最佳分解,所以F(12)=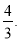
(1)求F(18)-F(16)的值;
(2)若正整数
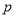 是4的倍数,我们称正整数
是4的倍数,我们称正整数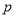 为“四季数”,如果一个两位正整数
为“四季数”,如果一个两位正整数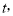
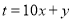 (
(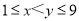 ,
,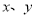 为自然数),交换个位上的数字与十位上的数字得到的新两位正整数减去原来的两位正整数所得的差为“四季数”,那么我们称这个数
为自然数),交换个位上的数字与十位上的数字得到的新两位正整数减去原来的两位正整数所得的差为“四季数”,那么我们称这个数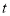 为“有缘数”,求所有“有缘数”中
为“有缘数”,求所有“有缘数”中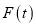 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形
 中,
中,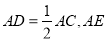 平分
平分 交
交 于点
于点 ,给出以下结论:①
,给出以下结论:① 为等腰直角三角形;②
为等腰直角三角形;② 为等边三角形;③
为等边三角形;③ ;④
;④ ⑤
⑤ 是
是 的中位线.其中正确的结论有( )
的中位线.其中正确的结论有( )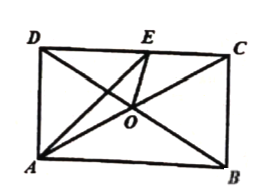
A.
 个B.
个B. 个C.
个C. 个D.
个D. 个
个 -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,A(a,0),C(0,c)且满足:(a+6)2+
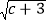 =0,长方形ABCO在坐标系中(如图),点O为坐标系的原点.
=0,长方形ABCO在坐标系中(如图),点O为坐标系的原点.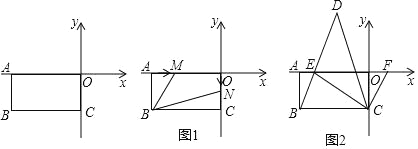
(1)求点B的坐标.
(2)如图1,若点M从点A出发,以2个单位/秒的速度向右运动(不超过点O),点N从原点O出发,以1个单位/秒的速度向下运动(不超过点C),设M、N两点同时出发,在它们运动的过程中,四边形MBNO的面积是否发生变化?若不变,求其值;若变化,求变化的范围.
(3)如图2,E为x轴负半轴上一点,且∠CBE=∠CEB,F是x轴正半轴上一动点,∠ECF的平分线CD交BE的延长线于点D,在点F运动的过程中,请探究∠CFE与∠D的数量关系,并说明理由
-
科目: 来源: 题型:
查看答案和解析>>【题目】【知识链接】 有理化因式:两个含有根式的非零代数式相乘,如果它们的积不含有根式,那么这两个代数式相互叫做有理化因式.
例如: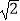 的有理化因式是
的有理化因式是 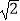 ;1﹣
;1﹣ 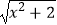 的有理化因式是1+
的有理化因式是1+ 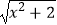 .
.
分母有理化:分母有理化又称“有理化分母”,也就是把分母中的根号化去.指的是如果代数式中分母有根号,那么通常将分子、分母同乘以分母的有理化因式,达到化去分母中根号的目的.如: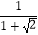 =
= 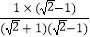 =
= 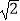 ﹣1,
﹣1, 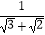 =
= 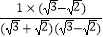 =
= 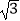 ﹣
﹣ 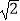 .
.
(1)【知识理解】 填空:2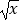 的有理化因式是;
的有理化因式是;
直接写出下列各式分母有理化的结果:
①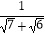 =;②
=;② 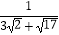 = .
= .
(2)【启发运用】 计算: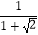 +
+ 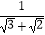 +
+ 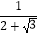 +…+
+…+ 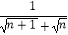 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】完成下列证明:如图,已知AD⊥BC,EF⊥BC,∠1=∠2.
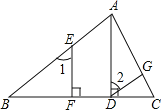
求证:DG∥BA.
证明:∵AD⊥BC,EF⊥BC(已知)
∴∠EFB=90°,∠ADB=90°(______)
∴∠EFB=∠ADB(等量代换)
∴EF∥AD(______)
∴∠1=∠BAD(______)
又∵∠1=∠2(已知)
∴∠______=∠______(等量代换)
∴DG∥BA.(______).
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解题: 学习了二次根式后,你会发现一些含有根号的式子可以写成另一个式子的平方,如3+2
 =(1+
=(1+  )2 , 我们来进行以下的探索:
)2 , 我们来进行以下的探索:
设a+b =(m+n
=(m+n  )2(其中a,b,m,n都是正整数),则有a+b
)2(其中a,b,m,n都是正整数),则有a+b  =m2+2n2+2mn
=m2+2n2+2mn  ,∴a=m+2n2 , b=2mn
,∴a=m+2n2 , b=2mn
, 这样就得出了把类似a+b 的式子化为平方式的方法.
的式子化为平方式的方法.
请仿照上述方法探索并解决下列问题:
(1)当a,b,m,n都为正整数时,若a﹣b =(m﹣n
=(m﹣n  )2 , 用含m,n的式子分别表示a,b,得a= , b=;
)2 , 用含m,n的式子分别表示a,b,得a= , b=;
(2)利用上述方法,找一组正整数a,b,m,n填空:﹣ =(﹣
=(﹣  )2
)2
(3)a﹣4 =(m﹣n
=(m﹣n  )2且a,m,n都为正整数,求a的值.
)2且a,m,n都为正整数,求a的值.
相关试题

