【题目】我们知道,任意一个正整数![]() 都可以进行这样的分解:
都可以进行这样的分解:![]() (
(![]() 是正整数,且
是正整数,且![]() ),在
),在![]() 的所有这种分解中,如果
的所有这种分解中,如果![]() 两因数之差的绝对值最小,我们就称
两因数之差的绝对值最小,我们就称![]() 是
是![]() 的最佳分解并规定:
的最佳分解并规定:![]() ,例如:12可以分解成1×12、2×6、3×4,因为:
,例如:12可以分解成1×12、2×6、3×4,因为:
![]() ,所以3×4是12的最佳分解,所以F(12)=
,所以3×4是12的最佳分解,所以F(12)=![]()
(1)求F(18)-F(16)的值;
(2)若正整数![]() 是4的倍数,我们称正整数
是4的倍数,我们称正整数![]() 为“四季数”,如果一个两位正整数
为“四季数”,如果一个两位正整数![]()
![]() (
(![]() ,
,![]() 为自然数),交换个位上的数字与十位上的数字得到的新两位正整数减去原来的两位正整数所得的差为“四季数”,那么我们称这个数
为自然数),交换个位上的数字与十位上的数字得到的新两位正整数减去原来的两位正整数所得的差为“四季数”,那么我们称这个数![]() 为“有缘数”,求所有“有缘数”中
为“有缘数”,求所有“有缘数”中![]() 的最小值.
的最小值.
参考答案:
【答案】(1)1;(2)![]()
【解析】
(1)根据题意求出F(18),F(16),的值代入求解;
(2)根据题意列出二元一次方程,解的所有可能性,求出F(t)的最小值.
(1)
∵18=3×6,16=4×4
∴F(18)=2,F(16)=1
∴F(18)-F(16)=1,
(2)依题意
10y+x-(10x+y)=4k,(k为整数)
∴9(y-x)=4k
∴y-x=4或8
且![]()
∴y=5,x=1;
y=6,x=2;
y=7,x=3;
y=8,x=4;
y=5,x=1;
y=9,x=5;
y=9,x=1;
∴两位正整数为51、62、73、84、95、91
∴F(51)=![]() ,F(62)=
,F(62)=![]() ,F(73)=73,F(84)=
,F(73)=73,F(84)=![]() ,F(95)=
,F(95)=![]() ,F(91)=
,F(91)=![]()
∴最小值为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读与计算:请阅读以下材料,并完成相应的任务. 古希腊的几何学家海伦在他的《度量》一书中给出了利用三角形的三边求三角形面积的“海伦公式”:如果一个三角形的三边长分别为a、b、c,设p=
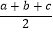 ,则三角形的面积S=
,则三角形的面积S= 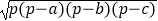 .
.
我国南宋著名的数学家秦九韶,曾提出利用三角形的三边求面积的“秦九韶公式”(三斜求积术):如果一个三角形的三边长分别为a、b、c,则三角形的面积S=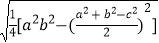 .
.
(1)若一个三角形的三边长分别是5,6,7,则这个三角形的面积等于 .
(2)若一个三角形的三边长分别是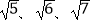 ,求这个三角形的面积.
,求这个三角形的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题,原命题和它的逆命题都是真命题的是( )
A.若
 ,则
,则
B.若三角形的三条边分别为
 ,则这个三角形是直角三角形
,则这个三角形是直角三角形C.正方形的四条边都相等
D.对角线互相垂直平分的四边形是菱形
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂计划生产A、B两种产品共50件,需购买甲、乙两种材料.生产一件A产品需甲种材料30千克、乙种材料10千克;生产一件B产品需甲、乙两种材料各20千克.经测算,购买甲、乙两种材料各1千克共需资金40元,购买甲种材料2千克和乙种材料3千克共需资金105元.
(1)甲、乙两种材料每千克分别是多少元?
(2)现工厂用于购买甲、乙两种材料的资金不超过38000元,且生产B产品不少于28件,问符合条件的生产方案有哪几种?
(3)在(2)的条件下,若生产一件A产品需加工费200元,生产一件B产品需加工费300元,应选择哪种生产方案,使生产这50件产品的成本最低?(成本=材料费+加工费)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形
 中,
中,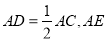 平分
平分 交
交 于点
于点 ,给出以下结论:①
,给出以下结论:① 为等腰直角三角形;②
为等腰直角三角形;② 为等边三角形;③
为等边三角形;③ ;④
;④ ⑤
⑤ 是
是 的中位线.其中正确的结论有( )
的中位线.其中正确的结论有( )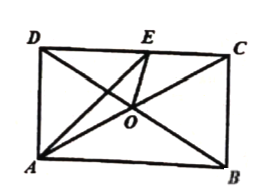
A.
 个B.
个B. 个C.
个C. 个D.
个D. 个
个 -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,A(a,0),C(0,c)且满足:(a+6)2+
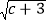 =0,长方形ABCO在坐标系中(如图),点O为坐标系的原点.
=0,长方形ABCO在坐标系中(如图),点O为坐标系的原点.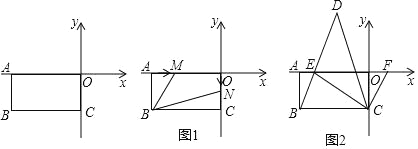
(1)求点B的坐标.
(2)如图1,若点M从点A出发,以2个单位/秒的速度向右运动(不超过点O),点N从原点O出发,以1个单位/秒的速度向下运动(不超过点C),设M、N两点同时出发,在它们运动的过程中,四边形MBNO的面积是否发生变化?若不变,求其值;若变化,求变化的范围.
(3)如图2,E为x轴负半轴上一点,且∠CBE=∠CEB,F是x轴正半轴上一动点,∠ECF的平分线CD交BE的延长线于点D,在点F运动的过程中,请探究∠CFE与∠D的数量关系,并说明理由
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥EF,∠C=90°,∠B,∠D,∠E三个角的大小分别是x,y,z则x,y,z之间满足的关系式是( )
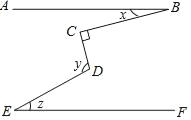
A. x+z=yB. x+y+═180°C. x+y﹣z=90°D. y+z﹣x=180°
相关试题

