Question

【题目】综合与实践

问题背景：

我们知道，三角形的中位线平行于三角形的第三边，并且等于第三边的一半，如何证明三角形中位线定理呢?

已知：如图1，在中，分别是的中点．

求证：

问题中既要证明两条线段所在的直线平行，又要证明其中一条线段的长等于另一线段长的一半．所以可以用“倍长法”将延长一倍：延长到，使得，连接这样只需证明，且．由于是的中点，容易证明四边形、四边形是平行四边形，证明．．．

问题解决：

上述材料中“倍长法”体现的数学思想主要是_____． (填入选项前的字母代号即可)

A．数形结合思想 B．转化思想 C．分类讨论思想 D．方程思想

证明四边形是平行四边形的依据是

反思交流：

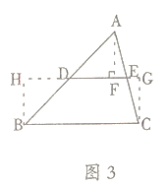
“智慧小组”在证明中位线定理时，在图1的基础上追加了如上辅助线作法：如图3，分别过点作的垂线，垂足分别为，．．

请你根据“智慧小组”添加的辅助线，证明三角形的中位线定理．

方法迁移：

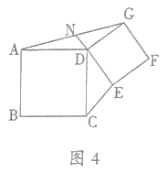
如图4、四边形和都是正方形，是的中点．求证：

Answer 1

【答案】（1）B；（2）一组对边平行且相等的四边形是平行四边形；（3）详见解析；（4）详见解析

【解析】

（1）根据解题方法知，将证明“”的问题转化为矩形的性质的问题；

（2）由平行四边形的判定定理填空；

（3）利用“”证明，根据全等三角形对应边相等可得，，同理，，则．然后判断出四边形是矩形，根据矩形的性质即可得到答案；

（4）如图4，延长到点，使得，连接、．易证，四边形是平行四边形，结合该平行四边形和图中正方形的性质，证得，故，所以．

（1）根据根据上述材料中“倍长法”体现的数学思想主要是转化思想．

故选：；

（2）证明四边形是平行四边形的依据是：一组对边平行且相等的四边形是平行四边形．

故答案为：一组对边平行且相等的四边形是平行四边形

（3）证明：如图3，

在和中，

，

∴，

∴，，

同理可得，，

∴，

又∵，

∴，

∴四边形是矩形，

∴，

∴．

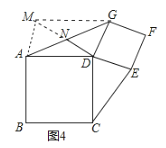
如图4，延长到点，使得连接，，

是的中点，

∴，

∴四边形是平行四边形，

∴，

∴，

四边形和都是正方形，

∴

∴

∴

在和中

，

∴，

∴，