【题目】如图1,直线![]() 分别与y轴、x轴交于点A、点B,点C的坐标为(-3,0),D为直线AB上一动点,连接CD交y轴于点E.
分别与y轴、x轴交于点A、点B,点C的坐标为(-3,0),D为直线AB上一动点,连接CD交y轴于点E.
(1) 点B的坐标为__________,不等式![]() 的解集为___________
的解集为___________
(2) 若S△COE=S△ADE,求点D的坐标;
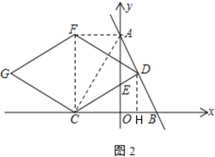
(3) 如图2,以CD为边作菱形CDFG,且∠CDF=60°.当点D运动时,点G在一条定直线上运动,请求出这条定直线的解析式.


参考答案:
【答案】(1)(3,0)、x<3;(2)∴D(![]() );(3)
);(3)![]()
【解析】(1)用坐标轴上点的特点及不等式的解法求解即可;(2)设点D 的纵坐标
为![]() ,由S△COE=S△ADE可得S△AOB=S△CBD,求出
,由S△COE=S△ADE可得S△AOB=S△CBD,求出![]() ,进而求出
,进而求出![]() ;(3) 连接CF, AC由全等三角形的判定可得△CAF≌△CBD得到AF∥x轴,设出点D 的坐标结合直线
;(3) 连接CF, AC由全等三角形的判定可得△CAF≌△CBD得到AF∥x轴,设出点D 的坐标结合直线![]() 得到关于m的方程,进而求解.
得到关于m的方程,进而求解.
(1) (3,0)、x<3
(2) ∵S△COE=S△ADE
∴S△AOB=S△CBD
即![]() ,yD=
,yD=![]()
当y=![]() 时,
时,![]()
∴D(![]() )
)
(3) 连接CF
∵∠CDF=60°
∴△CDF为等边三角形
连接AC
∵AB=AC=BC=6
∴△ABC为等边三角形
∴△CAF≌△CBD(SAS)
∴∠CAF=∠ACB=60°
∴AF∥x轴
设D(m,![]() )
)
过点D作DH⊥x轴于H
∴BH=3-m,DB=6-2m=AF
∴F(2m-6,![]() )
)
由平移可知:G(m-9,![]() )
)
令![]()
∴点G在直线![]() 上.
上.
-
科目: 来源: 题型:
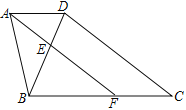
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,AB=3,BC=5,连接BD,∠BAD的平分线分别交BD、BC于点E、F,且AE∥CD
(1) 求AD的长;
(2) 若∠C=30°,求CD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂现有甲种原料360千克,乙种原料290千克,计划利用这两种原料生产A、B两种产品共50件.已知生产一件A种产品需用甲种原料9千克、乙种原料3千克,可获利润700元;生产一件B种产品需用甲种原料4千克、乙种原料10千克,可获利润1200元。设生产A种产品的生产件数为x, A、B两种产品所获总利润为y (元)
(1)试写出y与x之间的函数关系式;
(2)求出自变量x的取值范围;
(3)利用函数的性质说明哪种生产方案获总利润最大?最大利润是多少?
-
科目: 来源: 题型:
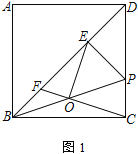
查看答案和解析>>【题目】已知:在正方形ABCD中,AB=6,P为边CD上一点,过P点作PE⊥BD于点E,连接BP.
(1)O为BP的中点,连接CO并延长交BD于点F
①如图1,连接OE,求证:OE⊥OC;
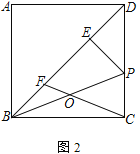
②如图2,若
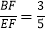 ,求DP的长;
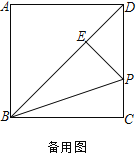
,求DP的长;(2)
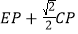 =___________
=___________
-
科目: 来源: 题型:
查看答案和解析>>【题目】(原题)已知直线AB∥CD,点P为平行线AB,CD之间的一点.如图1,若∠ABP=50°,∠CDP=60°,BE平分∠ABP,DE平分∠CDP,求∠BED的度数.
(探究)如图2,当点P在直线AB的上方时,若∠ABP=α,∠CDP=β,∠ABP和∠CDP的平分线交于点E1,∠ABE1与∠CDE1的角平分线交于点E2,∠ABE2与∠CDE2的角平分线交于点E3,…以此类推,求∠En的度数.
(变式)如图3,∠ABP的角平分线的反向延长线和∠CDP的补角的角平分线交于点E,试猜想∠P与∠E的数量关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】商家常将两种糖混合成“什锦糖”出售.对“什锦糖”的定价用以下方法确定:
若A种糖的单价为a元/千克,B种糖的单价为b元/千克(a≠b),则m千克的A种糖与n千克的B种糖混合而成的“什锦糖”单价为
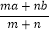 元.
元.(1)当a=20,b=30时,
①将10千克的A种糖与15千克的B种糖混合而成的“什锦糖”单价为多少?
②在①的基础上,若要将“什锦糖”单价提高2元,则需增加B种糖多少千克?
(2)若现有两种“什锦糖”:一种是由10千克的A种糖和10千克的B种糖混合而成,另一种是由100元价值的A种糖和100元价值的B种糖混合而成,则这两种“什锦糖”的单价哪一种更大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学对本校500名毕业生中考体育测试情况进行调查,根据男生及女生身体机能类选考坐位体前屈测试成绩整理,绘制成如下不完整的统计图(图①,图②)

请根据统计图提供的信息,回答下列问题:
(1)该校毕业生中男生有人,女生有人;
(2)扇形统计图中a= , b= , 并补全条形统计图;
(3)求图①中“8分a%”所对应的扇形圆心角的度数;
(4)若该校毕业生中随机抽取一名学生,则这名男生身体机能类选考坐位体前屈测试成绩为10分的概率是多少?
相关试题

