【题目】如图,AB为⊙O的直径,点C在⊙O外,∠ABC的平分线与⊙O交于点D,∠C=90°.
(1)CD与⊙O有怎样的位置关系?请说明理由;
(2)若∠CDB=60°,AB=6,求![]() 的长.
的长.

参考答案:
【答案】(1)相切,理由见解析;(2)π.
【解析】
(1)连接OD,根据BD是∠ABC的平分线的性质有∠CBD=∠ABD,根据OD=OB,得到∠ODB=∠ABD,等量代换得到∠ODB=∠CBD,根据平行线的判定得到OD∥CB,根据平行线的性质有∠ODC=∠C=90°,即可证明CD与⊙O相切;
(2)根据扇形的弧长公式进行计算即可.
(1)相切.理由如下:
连接OD,
∵BD是∠ABC的平分线,
∴∠CBD=∠ABD,
又∵OD=OB,
∴∠ODB=∠ABD,
∴∠ODB=∠CBD,
∴OD∥CB,
∴∠ODC=∠C=90°,
∴CD与⊙O相切;
(2)若∠CDB=60°,可得∠ODB=30°,
∴∠AOD=60°,
又∵AB=6,
∴AO=3,
∴![]()
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以G(0,1)为圆心,半径为2的圆与x轴交于A、B两点,与y轴交于C,D两点,点E为⊙O上一动点,CF⊥AE于F,则弦AB的长度为________;点E在运动过程中,线段FG的长度的最小值为________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上一点,且AP=AC.
(1)求证:PA是⊙O的切线;
(2)若PD=
 ,求⊙O的直径.
,求⊙O的直径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)一般地,数轴上表示数m和数n的两点之间的距离等于
 .如果表示数a和
.如果表示数a和 的两点之间的距离是5,那么
的两点之间的距离是5,那么 __________;
__________;(2)若数轴上表示数a的点位于
 与6之间,求
与6之间,求 的值;
的值;(3)当a取何值时,
 的值最小,最小值是多少?请说明理由.
的值最小,最小值是多少?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, ,点P从点B出发,以
,点P从点B出发,以 速度沿
速度沿 向点C运动,设点P的运动时间为t秒.
向点C运动,设点P的运动时间为t秒.(1)
 _______
_______ .(用含t的代数式表示)
.(用含t的代数式表示)(2)当点P从点B开始运动,同时,点Q从点C出发,以
 的速度沿
的速度沿 向点A运动,当
向点A运动,当 ≌
≌ 时,求v的值.
时,求v的值.(3)在(2)的条件下,求
 ≌
≌ 时v的值.
时v的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB=AC=8,∠BAC=90,直线l与以AB为直径的⊙O相切于点B,点D是直线l上任意一动点,连结DA交⊙O点E.
(1)当点D在AB上方且BD=6时,求AE的长;
(2)当CE恰好与⊙O相切时,求BD的长为多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,D是△ABC外接圆上的动点,且B,D位于AC的两侧,DE⊥AB,垂足为E,DE的延长线交此圆于点F.BG⊥AD,垂足为G,BG交DE于点H,DC,FB的延长线交于点P,且PC=PB.
(1)求证:BG∥CD;
(2)设△ABC外接圆的圆心为O,若AB=
 DH,∠OHD=80°,求∠BDE的大小.
DH,∠OHD=80°,求∠BDE的大小.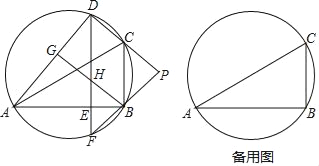
相关试题

