【题目】如图,AB=AC=8,∠BAC=90,直线l与以AB为直径的⊙O相切于点B,点D是直线l上任意一动点,连结DA交⊙O点E.
(1)当点D在AB上方且BD=6时,求AE的长;
(2)当CE恰好与⊙O相切时,求BD的长为多少?

参考答案:
【答案】(1)AE=![]() ;(2)BD= 4.
;(2)BD= 4.
【解析】
(1)连接BE,在Rt△ABD中,利用勾股定理求出AD的长,进而利用直角三角形等面积求出BE的长,在Rt△ABE中,利用勾股定理即可求出AE的长。
(2)连接OC,证明△ABD≌△CAO,根据全等三角形的性质即可求出BD的长.
解:(1)∵AB为直径,
∴∠AEB=90°,
∵BD为切线,
∴AB⊥BD,
∴∠ABD=90°,
在Rt△ABD中, ![]()
∵![]()
∴![]()
在Rt△ABE中, ![]()
(2)连接OC,如图,
∵∠BAC=90°,
∴CA为⊙O的切线,
∵CE为⊙O的切线,
∴CA=CE,
而OA=OE,
∴OC垂直平分AE,
∴∠1+∠3=90°,
而∠1+∠2=90°,
∴∠2=∠3,
而AB=CA,∠CAO=∠ABD,
∴△ABD≌△CAO,
∴BD=AO=4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)一般地,数轴上表示数m和数n的两点之间的距离等于
 .如果表示数a和
.如果表示数a和 的两点之间的距离是5,那么
的两点之间的距离是5,那么 __________;
__________;(2)若数轴上表示数a的点位于
 与6之间,求
与6之间,求 的值;
的值;(3)当a取何值时,
 的值最小,最小值是多少?请说明理由.
的值最小,最小值是多少?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,点C在⊙O外,∠ABC的平分线与⊙O交于点D,∠C=90°.
(1)CD与⊙O有怎样的位置关系?请说明理由;
(2)若∠CDB=60°,AB=6,求
 的长.
的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, ,点P从点B出发,以
,点P从点B出发,以 速度沿
速度沿 向点C运动,设点P的运动时间为t秒.
向点C运动,设点P的运动时间为t秒.(1)
 _______
_______ .(用含t的代数式表示)
.(用含t的代数式表示)(2)当点P从点B开始运动,同时,点Q从点C出发,以
 的速度沿
的速度沿 向点A运动,当
向点A运动,当 ≌
≌ 时,求v的值.
时,求v的值.(3)在(2)的条件下,求
 ≌
≌ 时v的值.
时v的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,D是△ABC外接圆上的动点,且B,D位于AC的两侧,DE⊥AB,垂足为E,DE的延长线交此圆于点F.BG⊥AD,垂足为G,BG交DE于点H,DC,FB的延长线交于点P,且PC=PB.
(1)求证:BG∥CD;
(2)设△ABC外接圆的圆心为O,若AB=
 DH,∠OHD=80°,求∠BDE的大小.
DH,∠OHD=80°,求∠BDE的大小.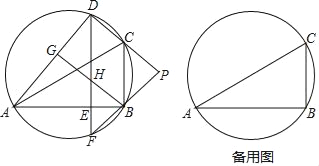
-
科目: 来源: 题型:
查看答案和解析>>【题目】用适当的方法解下列方程:
(1)4(x-1)2=100
(2)x2-2x-15=0
(3)3x2-13x-10=0
(4)3(x-3)2+x(x-3)=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线, DE⊥AB于点E.

(1)如图1,连接EC,求证:△EBC是等边三角形;
(2)点M是线段CD上的一点(不与点C,D重合),以BM为一边,在BM的下方作∠BMG=60°,MG交DE延长线于点G.请你在图2中画出完整图形,并直接写出MD,DG与AD之间的数量关系;
(3)如图3,点N是线段AD上的一点,以BN为一边,在BN的下方作∠BNG=60°,NG交DE延长线于点G,且MB=MG.试探究ND,DG与AD数量之间的关系,并说明理由.
相关试题

