【题目】如图,以G(0,1)为圆心,半径为2的圆与x轴交于A、B两点,与y轴交于C,D两点,点E为⊙O上一动点,CF⊥AE于F,则弦AB的长度为________;点E在运动过程中,线段FG的长度的最小值为________.

参考答案:
【答案】2![]()
![]() ﹣1
﹣1
【解析】
连接AC,AG,由OG垂直于AB,利用垂径定理得到O为AB的中点,由G的坐标确定出OG的长,在直角三角形AOG中,由AG与OG的长,利用勾股定理求出AO的长,进而确定出AB的长,由CG+GO求出OC的长,在直角三角形AOC中,利用勾股定理求出AC的长,由CF垂直于AE,得到三角形ACF始终为直角三角形,点F的运动轨迹为以AC为直径的半径,当点![]() 三点在同一条直线上时,线段FG的长度有最小值,根据
三点在同一条直线上时,线段FG的长度有最小值,根据![]() 求解即可.
求解即可.
连接AC,AG,

∵GO⊥AB,
∴O为AB的中点,即![]()
∵G(0,1),即OG=1,
∴在Rt△AOG中,根据勾股定理得:![]()
∴![]()
又CO=CG+GO=2+1=3,
∴在Rt△AOC中,根据勾股定理得:![]()
∵CF⊥AE,
∴△ACF始终是直角三角形,点F的运动轨迹为以AC为直径的半圆,
AC的中点为![]()
当点![]() 三点在同一条直线上时,线段FG的长度有最小值,
三点在同一条直线上时,线段FG的长度有最小值,
![]()
![]()
![]()
![]()
故答案为:(1). 2![]() (2).
(2). ![]() ﹣1
﹣1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠BAC=50°,∠C=70°,求∠DAC和∠BOA的度数

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线a、b、c表示三条公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有_______处.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:已知等边△ABC中,D是AC的中点,E是BC延长线上的一点,且CE=CD,DM⊥BC,垂足为M.
(1)求∠E的度数.
(2)求证:M是BE的中点.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上一点,且AP=AC.
(1)求证:PA是⊙O的切线;
(2)若PD=
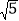 ,求⊙O的直径.
,求⊙O的直径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)一般地,数轴上表示数m和数n的两点之间的距离等于
 .如果表示数a和
.如果表示数a和 的两点之间的距离是5,那么
的两点之间的距离是5,那么 __________;
__________;(2)若数轴上表示数a的点位于
 与6之间,求
与6之间,求 的值;
的值;(3)当a取何值时,
 的值最小,最小值是多少?请说明理由.
的值最小,最小值是多少?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,点C在⊙O外,∠ABC的平分线与⊙O交于点D,∠C=90°.
(1)CD与⊙O有怎样的位置关系?请说明理由;
(2)若∠CDB=60°,AB=6,求
 的长.
的长.
相关试题

