【题目】知识再现:已知,如图,四边形ABCD是正方形,点M、N分别在边BC、CD上,连接AM、AN、MN,∠MAN=45°,延长CB至G使BG=DN,连接AG,根据三角形全等的知识,我们可以证明MN=BM+DN.
知识探究:(1)在如图中,作AH⊥MN,垂足为点H,猜想AH与AB有什么数量关系?并证明;
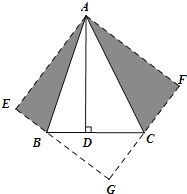
知识应用:(2)如图,已知∠BAC=45°,AD⊥BC于点D,且BD=2,AD=6,则CD的长为 ;
知识拓展:(3)如图,四边形ABCD是正方形,E是边BC的中点,F为边CD上一点,∠FEC=2∠BAE,AB=24,求DF的长.

参考答案:
【答案】(1)AB=AH, 证明见解析;(2)3;(3)8 .
【解析】
(1)先证△ABG≌△ADN,再证△GAM≌△NAM,根据GM和NM是对应边,得到AB=AH(全等三角形对应边上的高相等);
(2)作△ABD关于直线AB的对称△ABE,作△ACD关于直线AC的对称△ACF,延长EB、FC交于点G,则四边形AEGF是矩形,又AE=AD=AF,所以四边形AEGF是正方形,设设CD=x,则BG=62=4;CG=6 x;BC=2+ x,在Rt△BGC中,![]() 得x=3,所以CD的长为3.
得x=3,所以CD的长为3.
(3)过点A作![]() 交EF于点M,证明△ABE≌△AME,得到
交EF于点M,证明△ABE≌△AME,得到![]()
![]() 再证明
再证明![]() ≌
≌![]() ,设DF=x,得到EF=12+ x;FC=24 x;EC=12,在Rt△EFC中,
,设DF=x,得到EF=12+ x;FC=24 x;EC=12,在Rt△EFC中,![]() 解方程即可.
解方程即可.
(1)答:AB=AH,
证明:如图1
∵四边形ABCD是正方形,
∴![]()
∴![]()
又∵AB=AD,
∵在△ABG和△ADN中,

∴△ABG≌△ADN(SAS),
∴![]()
∵![]()
∴![]()
∴![]()
即![]()
∵在△GAM和△NAM中,
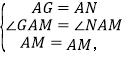
∴△GAM≌△NAM(SAS),
又∵GM和NM是对应边,
∴AB=AH(全等三角形对应边上的高相等);
(2)作△ABD关于直线AB的对称△ABE,作△ACD关于直线AC的对称△ACF,
∵AD是△ABC的高,
∴![]()
∴![]()
又∵![]()
∴![]()
延长EB、FC交于点G,则四边形AEGF是矩形,
又∵AE=AD=AF
∴四边形AEGF是正方形,
由(1)、(2)知:EB=DB=2,AE=AF=AD=EG=6,
设CD=x,
∴BG=62=4;CG=6 x;BC=2+ x,
在Rt△BGC中,![]()
解得![]()
故CD的长为3.

(3)如图3,过点A作![]() 交EF于点M,
交EF于点M,
![]()
![]()
![]()
在△ABE和△AME中,

∴△ABE≌△AME(AAS),
![]()
![]()
在![]() 和
和![]() 中,
中,
![]()
![]() ≌
≌![]() ,
,
![]()
设DF=x,
∴EF=12+ x/span>;FC=24 x;EC=12,
在Rt△EFC中,![]()
解得![]()
故DF的长为8.
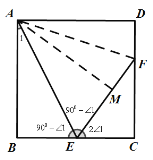
图3
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知某品牌的饮料有大瓶装与小瓶装之分.某超市花了3800元购进一批该品牌的饮料共1000瓶,其中大瓶和小瓶饮料的进价及售价如下表所示:
大瓶
小瓶
进价(元/瓶)
5
2
售价(元/瓶)
7
3
(1)该超市购进大瓶和小瓶饮料各多少瓶?
(2)在大瓶饮料售出200瓶,小瓶饮料售出100瓶后,商家决定将剩下的小瓶饮料的售价降低0.5元销售,并把其中一定数量的小瓶饮料作为赠品,在顾客一次性购买大瓶饮料时,每满2瓶就送1瓶小瓶饮料,送完即止.超市要使这批饮料售完后获得的利润不低于1250元,那么小瓶饮料作为赠品最多只能送出多少瓶?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,∠MON =70°,点A、B在∠MON的两条边上运动,∠MAB与∠NBA的平分线交于点P.
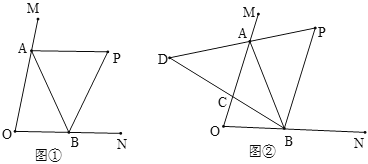
(1)点A、B在运动过程中,∠P的大小会变吗?若不会,求∠P的度数;若会,请说明理由.
(2)如图②,继续作BC平分∠ABO,AP的反向延长线交BC的延长线于点D,点A、B在运动过程中,∠D的大小会变吗?若不会,求出∠D的度数;若会,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】提出问题:
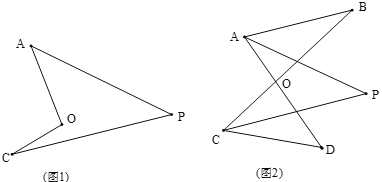
(1)如图,我们将图(1)所示的凹四边形称为“镖形”.在“镖形”图中,∠AOC与∠A、∠C、∠P的数量关系为_______.
(2)如图(2),已知AP平分∠BAD,CP平分∠BCD,∠B =28°,∠D=48°.求∠P的度数.
由(1)结论得:∠AOC =∠PAO +∠PCO+∠P
所以2∠AOC=2∠PAO +2∠PCO+2∠P即2∠AOC =∠BAO +∠DCO+2∠P
因为∠AOC =∠BAO +∠B,∠AOC =∠DCO +∠D
所以2∠AOC=∠BAO +∠DCO+∠B +∠D
所以∠P=_______.
解决问题:
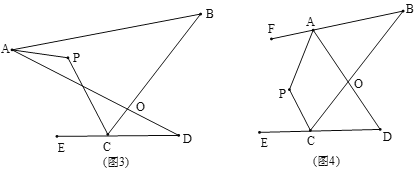
(3)如图(3),直线AP平分∠BAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的数量关系是_______;
(4)如图(4),直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的数量关系是_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )

A. 当AB=BC时,它是菱形 B. 当AC⊥BD时,它是菱形
C. 当∠ABC=90°时,它是矩形 D. 当AC=BD时,它是正方形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.
(1)求证:四边形BFCE是平行四边形;
(2)若AD=10,DC=3,∠EBD=60°,则BE= 时,四边形BFCE是菱形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
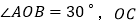 平分
平分 于
于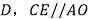 交OB于E
交OB于E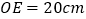 ,求CD的长.
,求CD的长.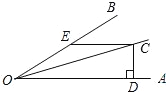
相关试题

