【题目】如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.
(1)求证:四边形BFCE是平行四边形;
(2)若AD=10,DC=3,∠EBD=60°,则BE= 时,四边形BFCE是菱形.

参考答案:
【答案】(1)证明见试题解析;(2)4.
【解析】试题分析:(1)由AE=DF,∠A=∠D,AB=DC,易证得△AEC≌△DFB,即可得BF=EC,∠ACE=∠DBF,且EC∥BF,即可判定四边形BFCE是平行四边形;
(2)当四边形BFCE是菱形时,BE=CE,根据菱形的性质即可得到结果.
试题解析:(1)∵AB=DC,∴AC=DB,
在△AEC和△DFB中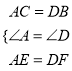 ,∴△AEC≌△DFB(SAS),
,∴△AEC≌△DFB(SAS),
∴BF=EC,∠ACE=∠DBF,∴EC∥BF,∴四边形BFCE是平行四边形;
(2)当四边形BFCE是菱形时,BE=CE,∵AD=10,DC=3,AB=CD=3,
∴BC=10﹣3﹣3=4,∵∠EBD=60°,∴BE=BC=4,
∴当BE="4" 时,四边形BFCE是菱形,
故答案为:4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学是从实际生活中来的,又应用于生活.请将下列事件与对应的数学原理连接起来.
事件
数学原理
教室的门要用两扇合页才能自由开关
直线外一点与直线上各点连线的所有线段中,垂线段最短
飞机从萧山飞往北京,它的航行路线是直的
经过两点有且只有一条直线
测量运动员的跳远成绩时,皮尺与起跳线保持垂直
两点之间线段最短
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,∠ABC的平分线交CD于点E.

(1)若∠A=70°,求∠ABE的度数;
(2)若AB∥CD,且∠1=∠2,判断DF和BE是否平行,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】现定义两种运算“⊕”“*”.对于任意两个整数,a⊕b=a+b-1,a*b=a×b-1,则(6⊕8)*(3⊕5)的结果是( )
A. 60 B. 90 C. 112 D. 69
-
科目: 来源: 题型:
查看答案和解析>>【题目】若代数式x+y的值是1,则代数式(x+y)2﹣x﹣y+1的值是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,AC=120cm,∠A=60°,点D从点C出发沿 CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒.过点D作DF⊥BC于点F,连接DE,EF.当四边形AEFD是菱形时,t的值为( )

A.20秒
B.18秒
C.12秒
D.6秒 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列解方程中正确的有
① x+4=﹣3,解得x=﹣
x+4=﹣3,解得x=﹣ 
②3x﹣5=7x,解得x=
③﹣(x﹣1)=﹣ (x+1),解得x=3
(x+1),解得x=3
④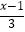 ﹣
﹣ 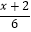 =
= 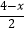 ,解得x=﹣8.
,解得x=﹣8.
相关试题

