【题目】如图,![]() 平分
平分![]() 于
于![]() 交OB于E
交OB于E![]() ,求CD的长.
,求CD的长.
参考答案:
【答案】10cm
【解析】试题分析:
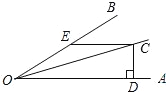
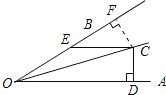
过点C作CF⊥OB于点F,由OC平分∠AOB,CD⊥OA可得CD=CF;由OC平分∠AOB,CE∥OA,可得∠EOC=∠DOC=∠ECO=15°,从而可得CE=OE=20cm,∠CEF=∠EOC+∠ECO=30°,结合CF⊥OB于点F可得CF=![]() CE=10cm,由此即可得到CD=10cm.
CE=10cm,由此即可得到CD=10cm.
试题解析:
如图,过点C作CF⊥OB于点F,
∵OC平分∠AOB,CD⊥OA,
∴CD=CF,∠EOC=∠DOC=15°,
∵CE∥OA,
∴∠EOC=∠DOC=∠ECO=15°,
∴CE=OE=20cm,∠CEF=∠EOC+∠ECO=30°,
又∵CF⊥OB于点F,
∴CF=![]() CE=10cm,
CE=10cm,
∴CD=10cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】知识再现:已知,如图,四边形ABCD是正方形,点M、N分别在边BC、CD上,连接AM、AN、MN,∠MAN=45°,延长CB至G使BG=DN,连接AG,根据三角形全等的知识,我们可以证明MN=BM+DN.
知识探究:(1)在如图中,作AH⊥MN,垂足为点H,猜想AH与AB有什么数量关系?并证明;
知识应用:(2)如图,已知∠BAC=45°,AD⊥BC于点D,且BD=2,AD=6,则CD的长为 ;
知识拓展:(3)如图,四边形ABCD是正方形,E是边BC的中点,F为边CD上一点,∠FEC=2∠BAE,AB=24,求DF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )

A. 当AB=BC时,它是菱形 B. 当AC⊥BD时,它是菱形
C. 当∠ABC=90°时,它是矩形 D. 当AC=BD时,它是正方形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.
(1)求证:四边形BFCE是平行四边形;
(2)若AD=10,DC=3,∠EBD=60°,则BE= 时,四边形BFCE是菱形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】“保护好环境,拒绝冒黑烟”荆州市公交公司将淘汰一条线路上“冒黑烟”较严重的公交车,计划购买
 型和
型和 型两种环保节能公交车
型两种环保节能公交车 辆,若购买
辆,若购买 型公交车
型公交车 辆,
辆, 型公交车
型公交车 辆,共需
辆,共需 万元,若购买
万元,若购买 型公交车
型公交车 辆,
辆, 型公交车
型公交车 辆,共需
辆,共需 万元.
万元.(1)求购买购买
 型和
型和 型公交车每辆多少钱?
型公交车每辆多少钱?(2)预计在该线路上
 型和
型和 型公交车每辆年均载客量分别为
型公交车每辆年均载客量分别为 万人次和
万人次和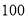 万人次,若该公司购买
万人次,若该公司购买 型和
型和 型公交车的总费用不超过
型公交车的总费用不超过 万元,且确保这
万元,且确保这 辆公交车在该线路上的年平均载客总和不少于
辆公交车在该线路上的年平均载客总和不少于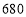 万人次,则该公司有哪几种购车方案?
万人次,则该公司有哪几种购车方案?(3)在(2)的条件下,哪种购车方案总费用最少?最少费用为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形ABCD中
 平分
平分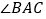 交BC于
交BC于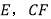 平分
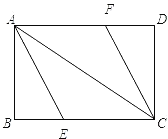
平分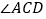 交AD于F.
交AD于F.(1)说明四边形AECF为平行四边形;
(2)求四边形AECF的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,OA=2,OB=3,现同时将点A,B分别向上平移2个单位,再向右平移2个单位,分别得到点A,B的对应点C,D,连接AC,BD.
(1)求点C、D的坐标及四边形ABDC的面积;
(2)若点Q在线的CD上移动(不包括C,D两点).QO与线段AB,CD所成的角∠1与∠2如图所示,给出下列两个结论:①∠1+∠2的值不变;②
 的值不变,其中只有一个结论是正确的,请你找出这个结论,并求出这个值.
的值不变,其中只有一个结论是正确的,请你找出这个结论,并求出这个值.(3)在y轴正半轴上是否存在点P,使得S△CDP=S△PBO?如果有,试求出点P的坐标.

相关试题

