【题目】如图,直线AB、CD相交于点O,OM⊥AB.
(1)若∠1=∠2,求∠NOD.
(2)若∠1=![]() ∠BOC,求∠AOC与∠MOD.
∠BOC,求∠AOC与∠MOD.

参考答案:
【答案】(1)∠NOD=90°;(2)∠AOC=45°,∠MOD=135°.
【解析】试题(1)由已知条件和观察图形可知∠1与∠AOC互余,再根据平角的定义求解;
(2)利用已知的∠1=![]() ∠BOC,结合图形以及对顶角的性质求∠AOC与∠MOD即可.
∠BOC,结合图形以及对顶角的性质求∠AOC与∠MOD即可.
试题解析:(1)因为OM⊥AB,
所以∠AOM=∠1+∠AOC=90°,
因为∠1=∠2,
所以∠NOC=∠2+∠AOC=90°,
所以∠NOD=180°-∠NOC=180°-90°=90°;
(2)因为OM⊥AB,
所以∠AOM=∠BOM=90°,
因为∠1=![]() ∠BOC,
∠BOC,
所以∠BOC=∠1+90°=3∠1,
解得∠1=45°,
所以∠AOC=90°-∠1=90°-45°=45°,
所以∠MOD=180°-∠1=180°-45°=135°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】乘法公式的探究及应用.
(1)如图1,可以求出阴影部分的面积是 (写成两数平方差的形式);
(2)如图2,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是 ,长是 ,面积是 (写成多项式乘法的形式);
(3)比较图1、图2两图的阴影部分面积,可以得到乘法公式 (用式子表达);
(4)运用你所得到的公式,计算下列各题:
①(2m+n-p)(2m-n+p);②10.3×9.7.

-
科目: 来源: 题型:
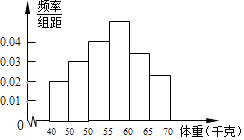
查看答案和解析>>【题目】为了解全区5000名初中毕业生的体重情况,随机抽测了400名学生的体重,频率分布如图所示(每小组数据可含最小值,不含最大值),其中从左至右前四个小长方形的高依次为0.02、0.03、0.04、0.05,由此可估计全区初中毕业生的体重不小于60千克的学生人数约为人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A,B两点的坐标分别为(2
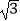 ,0),(0,10),M是△AOB外接圆⊙C上的一点,且∠AOM=30°,则点M的坐标为 .
,0),(0,10),M是△AOB外接圆⊙C上的一点,且∠AOM=30°,则点M的坐标为 . 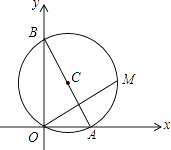
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题6分)如图,△ABC的顶点都在每个边长为1个单位长度的方格纸的格点上,将△ABC向右平移3格,再向上平移2格.
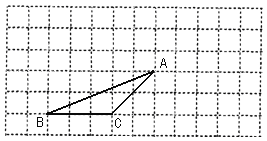
(1)请在图中画出平移后的
 ;
;(2)△ABC的面积为 _;
(3)若AB的长约为5.4,求出AB边上的高(结果保留整数).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在等腰△ABC中,其中AB=AC,∠A=40°,P是△ABC内一点,且∠1=∠2,则∠BPC等于( )

A. 110° B. 120° C. 130° D. 140°
-
科目: 来源: 题型:
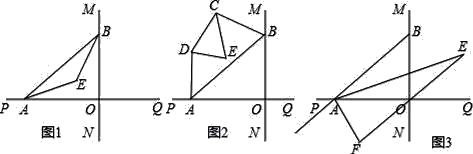
查看答案和解析>>【题目】直线MN与直线PQ垂直相交于O,点A在直线PQ上运动,点B在直线MN上运动.
(1)如图1,已知AE、BE分别是∠BAO和∠ABO角的平分线,点A、B在运动的过程中,∠AEB的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,试求出∠AEB的大小.
(2)如图2,已知AB不平行CD,AD、BC分别是∠BAP和∠ABM的角平分线,又DE、CE分别是∠ADC和∠BCD的角平分线,点A、B在运动的过程中,∠CED的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其值.
(3)如图3,延长BA至G,已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及延长线相交于E、F,在△AEF中,如果有一个角是另一个角的3倍,试求∠ABO的度数.
相关试题

