【题目】图中,用数字表示的∠1、∠2、∠3、∠4各角中,错误的判断是( )

A. 若将AC作为第三条直线,则∠1和∠3是同位角
B. 若将AC作为第三条直线,则∠2和∠4是内错角
C. 若将BD作为第三条直线,则∠2和∠4是内错角
D. 若将CD作为第三条直线,则∠3和∠4是同旁内角
参考答案:
【答案】B
【解析】
根据三线八角中三种角度判断要求:同位角形状像“F”,内错角形状像“Z”,同旁内角形状像“U”,以及每组角的公共边即为第三条直线判断即可.
A选项中∠1和∠3的公共边为AC,并且两角组成的图形像“F”,所以它们是同位角,故A正确;
B选项中∠2和∠4的公共边为BD,而题目中给出的第三边为AC,故B错误;
C选项中∠2和∠4的公共边为BD,并且两角组成的图形像“Z”,所以它们是内错角,故C正确;
D选项中∠3和∠4的公共边为CD,并且两角组成的图形像“U”,所以它们是同旁内角,故D正确.
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数
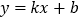 的图像经过点
的图像经过点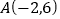 ,且与
,且与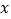 轴相交于点
轴相交于点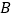 ,与正比例函数
,与正比例函数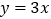 的图像交于点
的图像交于点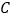 ,点
,点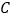 的横坐标为
的横坐标为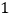 .
.(1)求
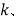
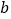 的值;
的值;(2)若点
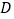 在
在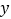 轴上,且满足
轴上,且满足 ,求点
,求点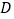 的坐标.
的坐标.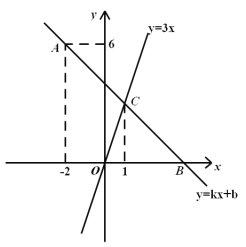
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形OABC的OA边在x轴的正半轴上,OC在y轴的正半轴上,抛物线y=ax2+bx经过点B(1,4)和点E(3,0)两点.

(1)求抛物线的解析式;
(2)若点D在线段OC上,且BD⊥DE,BD=DE,求D点的坐标;
(3)在条件(2)下,在抛物线的对称轴上找一点M,使得△BDM的周长为最小,并求△BDM周长的最小值及此时点M的坐标;
(4)在条件(2)下,从B点到E点这段抛物线的图象上,是否存在一个点P,使得△PAD的面积最大?若存在,请求出△PAD面积的最大值及此时P点的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】一辆汽车在直线形的公路上由A向B行驶,M、N分别是位于公路AB两侧的两个学校,如图.
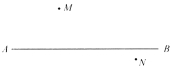
(1)汽车行驶时,会对公路两旁的学校都造成一定的影响,当汽车行驶到何处时,分别对两个学校影响最大?在图中标出来;
(2)当汽车从A向B行驶时,在哪一段上对两个学校影响越来越大?越来越小?对M学校影响逐渐减小而对N学校影响逐渐增大?
-
科目: 来源: 题型:
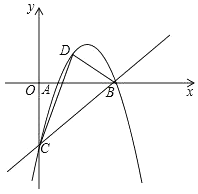
查看答案和解析>>【题目】如图,抛物线经过A(1,0),B(4,0),C(0,﹣4)三点,点D是直线BC上方的抛物线上的一个动点,连结DC,DB,则△BCD的面积的最大值是( )
A.7
B.7.5
C.8
D.9 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线a,b被直线c,d所截,直线a,c,d相交于点O,按要求完成下列各小题.
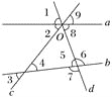
(1)在图中的∠1~∠9这9个角中,同位角共有多少对?请你全部写出来;
(2)∠4和∠5是什么位置关系的角?∠6和∠8之间的位置关系与∠4和∠5的相同吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】乘法公式的探究及应用.
(1)如图1,可以求出阴影部分的面积是 (写成两数平方差的形式);
(2)如图2,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是 ,长是 ,面积是 (写成多项式乘法的形式);
(3)比较图1、图2两图的阴影部分面积,可以得到乘法公式 (用式子表达);
(4)运用你所得到的公式,计算下列各题:
①(2m+n-p)(2m-n+p);②10.3×9.7.

相关试题

