【题目】某工厂有甲种原料360kg,乙种原料290kg,计划用这两种原料生产A、B两种产品共50件,已知生产一件A种产品,需用甲种原料9kg,乙种原料3kg,可获利润700元;生产一件B种产品,需用甲种原料4kg,乙种原料10kg,可获利润1200元.
(1)按要求安排A、B两种产品的生产件数,有哪几种方案?请你设计出来;
(2)设生产A、B两种产品总利润是W(元),采用哪种生产方案获总利润最大?最大利润为多少?
参考答案:
【答案】
(1)解:设安排生产A种产品x件,则生产B种产品(50﹣x)件,
根据题意有: ![]() ,
,
解得:30≤x≤32,
∵x为整数,
∴x30,31,32,
所以有三种方案:①安排A种产品30件,B种产品20件;
②安排A种产品31件,B种产品19件;
③安排A种产品32件,B种产品18件
(2)解:设安排生产A种产品x件,
那么利润为:w=700x+1200(50﹣x)=﹣500x+60000,
∵k=﹣500<0,
∴y随x的增大而减小,
∴当x=30时,对应方案的利润最大,y=﹣500×30+60000=45000,最大利润为45000元.
∴采用方案①所获利润最大,为45000元
【解析】(1)本题首先找出题中的等量关系即甲种原料不超过360千克,乙种原料不超过290千克,然后列出不等式组并求出它的解集.由此可确定出具体方案.(2)根据题意列出w与x之间的函数关系式,利用一次函数的增减性和(1)得到的取值范围即可求得最大利润.
【考点精析】解答此题的关键在于理解一元一次不等式组的应用的相关知识,掌握1、审:分析题意,找出不等关系;2、设:设未知数;3、列:列出不等式组;4、解:解不等式组;5、检验:从不等式组的解集中找出符合题意的答案;6、答:写出问题答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,按以下步骤作图:①分别以A、B为圆心,大于
 AB的长为半径画弧,两弧相交于点M、N;②作直线MN交AC于点D,连接BD.若CD=CB,∠A=35°,则∠C等于( )
AB的长为半径画弧,两弧相交于点M、N;②作直线MN交AC于点D,连接BD.若CD=CB,∠A=35°,则∠C等于( )
A. 40° B. 50° C. 60° D. 70°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四个正方形拼接成的图形中,以A1、A2、A3、…、A10这十个点中任意三点为顶点,共能组成个等腰直角三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】In right Fig.,if the length of the segment AB is 1,M is the midpoint of the segment AB,and point C divides the segment MB into two parts such that MC:CB=1:2,then the length of AC is 。
(英汉词典:length 长度;segment 线段;midpoint 中点;divides…into 分为,分成)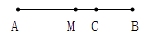
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在等边△ABC中,点D是BC边的中点,点P为AB 边上的一个动点,设AP=
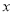 ,PD=
,PD= 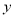 ,若
,若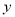 与
与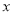 之间的函数关系的图象如图2所示,则等边△ABC的面积为( )
之间的函数关系的图象如图2所示,则等边△ABC的面积为( )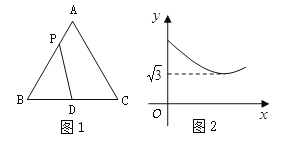
A. 4 B.
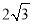 C. 12 D.
C. 12 D. 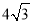
-
科目: 来源: 题型:
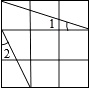
查看答案和解析>>【题目】如图,在3×3的正方形网格中标出了∠1和∠2。则∠1+∠2=。
-
科目: 来源: 题型:
查看答案和解析>>【题目】求x的值:(2x-3)2=36.
相关试题

