搜索
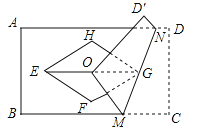
【题目】如图，矩形ABCD与菱形EFGH的对角线均交于点O，且EG∥BC，将矩形折叠，使点C与点O重合，折痕MN恰好过点G若AB=
，EF=2，∠H=120°，则DN的长为（ ）
A．
B．
C．
D．
参考答案：
【答案】C．
【解析】
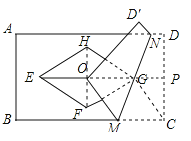
试题分析：长EG交DC于P点，连接GC、FH；如图所示：
则CP=DP=
CD=
，△GCP为直角三角形，∵四边形EFGH是菱形，∠EHG=120°，∴GH=EF=2，∠OHG=60°，EG⊥FH，∴OG=GHsin60°=2×
=
，由折叠的性质得：CG=OG=，OM=CM，∠MOG=∠MCG，∴PG=
=，∵OG∥CM，∴∠MOG+∠OMC=180°，∴∠MCG+∠OMC=180°，∴OM∥CG，∴四边形OGCM为平行四边形，∵OM=CM，∴四边形OGCM为菱形，∴CM=OG=，根据题意得：PG是梯形MCDN的中位线，∴DN+CM=2PG=
，∴DN=
；故选C．
-
科目： 来源： 题型：
查看答案和解析>>【题目】从泰州到某市，可乘坐普通列车或动车，已知动车的行驶路程是400千米，普通列车的行驶路程是动车的行驶路程的1.3倍．
（1）求普通列车的行驶路程；
（2）若动车的平均速度（千米/时）是普通列车平均速度（千米/时）的2.5倍，且乘坐动车所需时间比乘坐普通列车所需时间缩短3小时，求动车的平均速度．
-
科目： 来源： 题型：
查看答案和解析>>【题目】平面直角坐标系xOy中，已知函数y1=
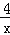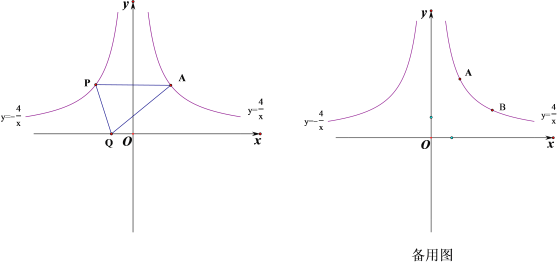
（x＞0）与y2=﹣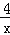（x＜0）的图象如图所示，点A、B是函数y1=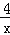（x＞0）图象上的两点，点P是y2=﹣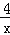（x＜0）的图象上的一点，且AP∥x轴，点Q是x轴上一点，设点A、B的横坐标分别为m、n（m≠n）．（1）求△APQ的面积；
（2）若△APQ是等腰直角三角形，求点Q的坐标；
（3）若△OAB是以AB为底的等腰三角形，求mn的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某文化用品商店用1 000元购进一批“晨光”套尺，很快销售一空；商店又用1 500元购进第二批该款套尺，购进时单价是第一批的
倍，所购数量比第一批多100套．（1）求第一批套尺购进时单价是多少？
（2）若商店以每套4元的价格将这两批套尺全部售出，可以盈利多少元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】用反证法证明“垂直于同一直线的两直线平行”第一步先假设（ ）
A.相交
B.两条直线不垂直
C.两条直线不同时垂直同一条直线
D.垂直于同一条直线的两条直线相交 -
科目： 来源： 题型：
查看答案和解析>>【题目】点P（2，3）关于x轴的对称点的坐标是（ ）
A.（-2，3）B.（2，-3）C.（2，3）D.（-2，-3）
-
科目： 来源： 题型：
查看答案和解析>>【题目】以下可以用来证明命题“任何偶数都是4的倍数”是假命题的反例为（ ）
A.3
B.4
C.8
D.6
相关试题
