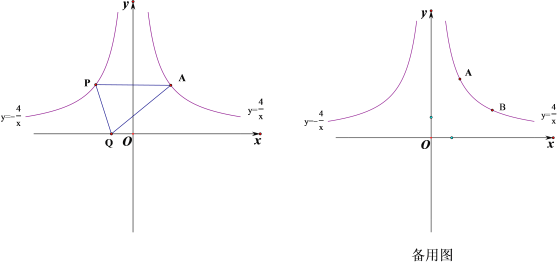
【题目】平面直角坐标系xOy中,已知函数y1=![]() (x>0)与y2=﹣
(x>0)与y2=﹣![]() (x<0)的图象如图所示,点A、B是函数y1=
(x<0)的图象如图所示,点A、B是函数y1=![]() (x>0)图象上的两点,点P是y2=﹣
(x>0)图象上的两点,点P是y2=﹣![]() (x<0)的图象上的一点,且AP∥x轴,点Q是x轴上一点,设点A、B的横坐标分别为m、n(m≠n).
(x<0)的图象上的一点,且AP∥x轴,点Q是x轴上一点,设点A、B的横坐标分别为m、n(m≠n).
(1)求△APQ的面积;
(2)若△APQ是等腰直角三角形,求点Q的坐标;
(3)若△OAB是以AB为底的等腰三角形,求mn的值.
参考答案:
【答案】(1)S=4(2)![]() (3)mn=4
(3)mn=4
【解析】试题分析:(1)由点A的横坐标为m,则A(m, ![]() ),P(-m,
),P(-m, ![]() ),过点P、A、Q分别作PM
),过点P、A、Q分别作PM![]() x轴交x轴于点M,PN
x轴交x轴于点M,PN![]() x轴交x轴于点N,QR
x轴交x轴于点N,QR![]() AP交AP轴于点R,可得出S矩形PMNA=8,由四边形PMQR和四边形ARQN是矩形可得:S△PQM=S△PRQ,S△ANQ=S△ARQ,所以S△APQ=S△PRQ+ S△ARQ=
AP交AP轴于点R,可得出S矩形PMNA=8,由四边形PMQR和四边形ARQN是矩形可得:S△PQM=S△PRQ,S△ANQ=S△ARQ,所以S△APQ=S△PRQ+ S△ARQ=![]() S矩形PMNA;(2)分情况讨论,当PQ
S矩形PMNA;(2)分情况讨论,当PQ![]() x轴时,求得
x轴时,求得![]() ,当PQ=AQ时
,当PQ=AQ时![]() ;(3)由OA=OB,解得mn=4.
;(3)由OA=OB,解得mn=4.
试题解析:
(1)过点P、A、Q分别作PM![]() x轴交x轴于点M,PN
x轴交x轴于点M,PN![]() x轴交x轴于点N,QR
x轴交x轴于点N,QR![]() AP轴交AP轴于点R,则四边形APMN、四边形PMQR、四边形ARQN是矩形,如图所示:
AP轴交AP轴于点R,则四边形APMN、四边形PMQR、四边形ARQN是矩形,如图所示:
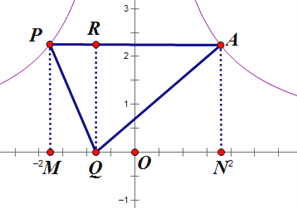
∵点A的横坐标为m,且在函数![]() 上,AP∥x轴,且点P在函数
上,AP∥x轴,且点P在函数![]() 上,
上,
∴点A(m, ![]() ),点P(-m,
),点P(-m, ![]() ),
),
∴MN=m-(-m)=2m,PM=![]() ,
,
∴S矩形PMNA=2m╳![]() =8,
=8,
∵四边形PMQR、四边形ARQN是矩形,
∴S△PQM=S△PRQ,S△ANQ=S△ARQ,
∴S△APQ=S△PRQ+ S△ARQ=![]() S矩形PMNA=4;
S矩形PMNA=4;
(2)当PQ![]() x轴时,则PQ=
x轴时,则PQ=![]() ,,AP=2m,
,,AP=2m,
∵PQ=AP
∴2m=![]() ,
,
∴m=![]()
∴![]() ,
,
当PQ=AQ时,则![]() ;
;
(3)∵△OAB是以AB为底的等腰三角形,
∴OA=OB,
∵A(m, ![]() ),B(n,
),B(n, ![]() ),
),
∴![]()
∴mn=4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果两个角的两边分别平行,而其中一个角比另一个角的4倍少30°,那么这两个角的度数分别______________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】花粉的质量很小,一粒某种花粉的质量约为0.000103毫克,那么0.000103可用科学记数法表示为( )
A. 10.3×10﹣5 B. 1.03×10﹣4 C. 0.103×10﹣3 D. 1.03×10﹣3
-
科目: 来源: 题型:
查看答案和解析>>【题目】从泰州到某市,可乘坐普通列车或动车,已知动车的行驶路程是400千米,普通列车的行驶路程是动车的行驶路程的1.3倍.
(1)求普通列车的行驶路程;
(2)若动车的平均速度(千米/时)是普通列车平均速度(千米/时)的2.5倍,且乘坐动车所需时间比乘坐普通列车所需时间缩短3小时,求动车的平均速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某文化用品商店用1 000元购进一批“晨光”套尺,很快销售一空;商店又用1 500元购进第二批该款套尺,购进时单价是第一批的
 倍,所购数量比第一批多100套.
倍,所购数量比第一批多100套.(1)求第一批套尺购进时单价是多少?
(2)若商店以每套4元的价格将这两批套尺全部售出,可以盈利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD与菱形EFGH的对角线均交于点O,且EG∥BC,将矩形折叠,使点C与点O重合,折痕MN恰好过点G若AB=
 ,EF=2,∠H=120°,则DN的长为( )
,EF=2,∠H=120°,则DN的长为( )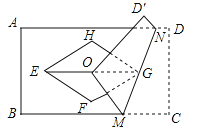
A.
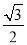 B.
B.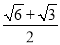 C.
C.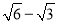 D.
D.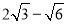
-
科目: 来源: 题型:
查看答案和解析>>【题目】用反证法证明“垂直于同一直线的两直线平行”第一步先假设( )
A.相交
B.两条直线不垂直
C.两条直线不同时垂直同一条直线
D.垂直于同一条直线的两条直线相交
相关试题

