【题目】如图是某货站传送货物的平面示意图. 为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°. 已知原传送带AB长为4米.
(1)求新传送带AC的长度;
(2)如果需要在货物着地点C的左侧留出2米的通道,试判断距离B点4米的货物![]() 是否需要挪走,并说明理由.
是否需要挪走,并说明理由.

参考答案:
【答案】(1)5.6m;(2)应挪走.
【解析】试题解析:试题分析:(1)在构建的直角三角形中,首先求出两个直角三角形的公共直角边,进而在Rt△ACD中,求出AC的长.
(2)通过解直角三角形,可求出BD、CD的长,进而可求出BC、PC的长.然后判断PC的值是否大于2米即可.
试题解析:(1)如图,
在Rt△ABD中,AD=ABsin45°=4![]() .
.
在Rt△ACD中,
∵∠ACD=30°,
∴AC=2AD=8.
即新传送带AC的长度约为8米;
(2)结论:货物MNQP不用挪走.
解:在Rt△ABD中,BD=ABcos45°=4![]() =4.
=4.
在Rt△ACD中,CD=![]() AD=4
AD=4![]() .
.
∴CB=CD-BD=4![]() -4≈2.8.
-4≈2.8.
∵PC=PB-CB≈5-2.8=2.2>2,
∴货物MNQP不应挪走.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(a+2b)(a+b)-3a(a+b)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,弦DF与半径OB相交于点P,连结EF、EO,若DE=
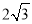 ,∠DPA=45°.
,∠DPA=45°.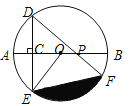
(1)求⊙O的半径;
(2)求图中阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:﹣1﹣(﹣1)0的结果正确是( )
A.0
B.1
C.2
D.﹣2 -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,将一块等腰直角三角板ABC放在第一象限,斜靠在两条坐标轴上,∠ACB=900 , 且A(0,4),点C(2,0),BE⊥x轴于点E,一次函数y=x+b经过点B,交y轴于点D。

(1)求证;△AOC≌△CEB
(2)求△ABD的面积。 -
科目: 来源: 题型:
查看答案和解析>>【题目】张老师和李老师住在同一个小区,离学校3000米,某天早晨,张老师和李老师分别于7点10分、7点15分离家骑自行车上班,刚好在校门口遇上,已知李老师骑车的速度是张老师的1.2倍,求他们各自骑自行车的速度分别是多少米/分?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,已知点A(﹣3,0)、B(0,4),对△OAB连续作翻转变换,依次得到△1、△2、△3、△4…,则△23中的
 的坐标为_______________。
的坐标为_______________。
相关试题

