【题目】如图1,△ABC是等腰直角三角形,∠BAC= 90°,AB=AC,四边形ADEF是正方形,点B、C分别在边AD、AF上,此时BD=CF,BD⊥CF成立.
(1)当△ABC绕点A逆时针旋转![]() (0°<
(0°<![]() <90°)时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.
<90°)时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.
(2)当△ABC绕点A逆时针旋转45°时,如图3,延长DB交CF于点H.
①求证: BD⊥CF. ② 当AB=2,AD=3,时,求线段BD的长.

参考答案:
【答案】(1)、证明过程见解析;(2)、①、证明过程见解析;②、![]()
【解析】
试题分析:(1)、根据旋转图形的性质得出AC=AB,∠CAF=∠BAD=θ,AF=AD,从而得出三角形全等;(2)、①、根据全等得出∠HFN=∠ADN,结合已知得出∠HFN+∠HNF=90°,从而得出结论;②、连接DF,延长AB,与DF交于点M,根据正方形的性质得出AM=DM,然后根据Rt△MAD的勾股定理得出答案.
试题解析:(l)、BD=CF成立.
由旋转得:AC=AB,∠CAF=∠BAD=θ;AF=AD, ∴△ABD≌△ACF, ∴BD=CF.
(2) ①、由(1)得,△ABD≌△ACF, ∴∠HFN=∠ADN, ∵∠HNF=∠AND,∠AND+∠AND=90°
∴∠HFN+∠HNF=90° ∴∠NHF=90°, ∴HD⊥HF,即BD⊥CF.
②、如图,连接DF,延长AB,与DF交于点M. ∵四边形ADEF是正方形 ∴∠MDA=45°∵∠MAD=45°
∴∠MAD=∠MDA,∠AMD=90°,∴AM=DM ∵AD=3 在△MAD中,![]() ∴AM=DM=3
∴AM=DM=3
.∴MB=AM-AB=3-2=1 在△BMD中,![]()
∴![]()

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程2x2+4x+m﹣1=0有两个相等的实数根,则m的值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b是关于x的一元二次方程x2﹣3x﹣1=0的两个实数根,则代数式3ab﹣a﹣b的值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若4anb3与﹣3a5bm﹣1是同类项,则m﹣n= .
-
科目: 来源: 题型:
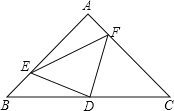
查看答案和解析>>【题目】已知:三角形ABC中,∠A=90,AB=AC,D为BC的中点,如图,E,F分别是AB,AC上的点,且BE=AF,求证:△DEF为等腰直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a﹣b=3,a+b=﹣2,则a2﹣b2=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个池塘的水浮莲,每天都在生长,且每天的面积是前一天的两倍。如果12天就能把整个池塘遮满,那么水浮莲长到遮住半个池塘需要( )
A. 6天 B. 8天 C. 10天 D. 11天
相关试题

