【题目】(1)阅读并回答:
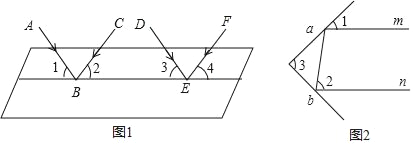
科学实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的角相等.如图1,一束平行光线AB与DE射向一个水平镜面后被反射,此时∠1=∠2,∠3=∠4.
由条件可知:∠1与∠3的大小关系是 ,理由是 ;∠2与∠4的大小关系是 ;
反射光线BC与EF的位置关系是 ,理由是 ;
(2)解决问题:
①如图2,一束光线m射到平面镜a上,被a反射到平面镜b上,又被b镜反射,若b反射出的光线n平行于m,且∠1=35°,则∠2= ,∠3= ;
在①中,若∠1=40°,则∠3= ,
由①②请你猜想:当∠3= 时,任何射到平面镜a上的光线m经过平面镜a和b的两次反射后,入射光线m与反射光线n总是平行的?请说明理由.
参考答案:
【答案】(1)①相等、两直线平行,同位角相等、相等;②平行、同位角相等,两直线平行.(2)①70°、90°;②90°;③90°.
【解析】
(1)根据平行线的判定与性质逐一求解;
(2)①根据入射角等于反射角得出∠1=∠4,∠5=∠7,求出∠6,根据平行线性质即可求出∠2,求出∠5,根据三角形内角和求出∠3即可;
②与①同理;
③求出∠4+∠5,求出∠1+∠4+∠5+∠7,即可求出∠2+∠6,根据平行线的判定推出即可.
(1)①由条件可知:∠1与∠3的大小关系是相等,理由是两直线平行,同位角相等;∠2与∠4的大小关系是相等;
②反射光线BC与EF的位置关系是平行,理由是同位角相等,两直线平行;
故答案为:①相等、两直线平行,同位角相等、相等;②平行、同位角相等,两直线平行.
(2)①如图,
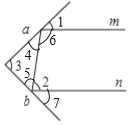
∵∠1=35°,
∴∠4=∠1=35°,
∴∠6=180°﹣35°﹣35°=110°,
∵m∥n,
∴∠2+∠6=180°,
∴∠2=70°,
∴∠5=∠7=55°,
∴∠3=180°﹣55°﹣35°=90°;
②在①中,若∠1=40°,则∠4=∠1=40°,
∴∠6=180°﹣40°﹣40°=100°,
∵m∥n,
∴∠2+∠6=180°,
∴∠2=80°,
∴∠5=∠7=50°,
∴∠3=180°﹣50°﹣40°=90°.
③猜想:当∠3=90°时,m总平行于n,
理由:∵三角形的内角和为180°,又∠3=90°,

∴∠4+∠5=90°.
∵∠4=∠1、∠5=∠7,
∴∠1+∠7=90°,
∴∠1+∠4+∠5+∠7=90°+90°=180°,
∵∠1+∠4+∠6+∠5+∠2+∠7=180°+180°=360°,
∴∠6+∠2=180°.
∴m∥n(同旁内角互补,而直线平行).
故答案为:①70°、90°;②90°;③90°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两块等腰直角三角形纸片AOB和COD按图①所示放置,直角顶点重合在点O处,AB=25.保持纸片AOB不动,将纸片COD绕点O逆时针旋转α(0°<α<90°)角度,如图②所示.
(1)在图②中,求证:AC=BD,且AC⊥BD;
(2)当BD与CD在同一直线上(如图③)时,若AC=7,求CD的长.



-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,过点B作⊙O的切线DE,F为射线BD上一点,连接CF.
(1)求证:∠CBE=∠A;
(2)若⊙O的直径为5,BF=2,tanA=2,求CF的长.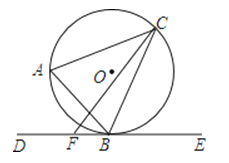
-
科目: 来源: 题型:
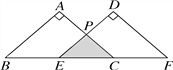
查看答案和解析>>【题目】已知△ABC是等腰直角三角形,AB=
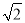 ,把△ABC沿直线BC向右平移得到△DEF.如果E是BC的中点,AC与DE交于P点,以直线BC为x轴,点E为原点建立直角坐标系.
,把△ABC沿直线BC向右平移得到△DEF.如果E是BC的中点,AC与DE交于P点,以直线BC为x轴,点E为原点建立直角坐标系.(1)求△ABC与△DEF的顶点坐标;
(2)判断△PEC的形状;
(3)求△PEC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,定义直线x=m与双曲线yn=
 的交点Am , n(m、n为正整数)为“双曲格点”,双曲线yn=
的交点Am , n(m、n为正整数)为“双曲格点”,双曲线yn= 在第一象限内的部分沿着竖直方向平移或以平行于x轴的直线为对称轴进行翻折之后得到的函数图象为其“派生曲线”.
在第一象限内的部分沿着竖直方向平移或以平行于x轴的直线为对称轴进行翻折之后得到的函数图象为其“派生曲线”.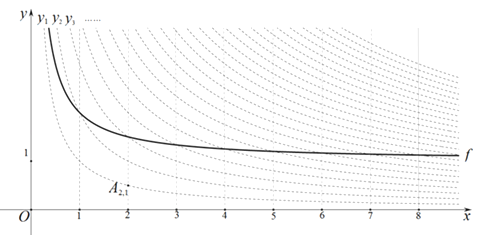
(1)①“双曲格点”A2 , 1的坐标为 ;②若线段A4 , 3A4 , n的长为1个单位长度,则n= ;
(2)图中的曲线f是双曲线y1=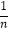 的一条“派生曲线”,且经过点A2 , 3 , 则f的解析式为y=
的一条“派生曲线”,且经过点A2 , 3 , 则f的解析式为y=
(3)画出双曲线y3=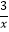 的“派生曲线”g(g与双曲线y3=
的“派生曲线”g(g与双曲线y3=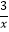 不重合),使其经过“双曲格点”A2 , a、A3 , 3、A4 , b .
不重合),使其经过“双曲格点”A2 , a、A3 , 3、A4 , b . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在△ABC中,AB=AC。

(1)若D为AC的中点,BD把三角形的周长分为24cm和30cm两部分,求△ABC三边的长;
(2)若D为AC上一点,试说明AC>
 (BD+DC)。
(BD+DC)。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠A=110°,∠B=85°将△BMN沿着MN翻折,得到△FMN,若MF∥AD,FN∥DC,则∠C的度数为( )
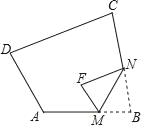
A. 70° B. 80° C. 90° D. 100°
相关试题

