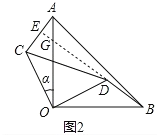
【题目】两块等腰直角三角形纸片AOB和COD按图①所示放置,直角顶点重合在点O处,AB=25.保持纸片AOB不动,将纸片COD绕点O逆时针旋转α(0°<α<90°)角度,如图②所示.
(1)在图②中,求证:AC=BD,且AC⊥BD;
(2)当BD与CD在同一直线上(如图③)时,若AC=7,求CD的长.



参考答案:
【答案】(1)见解析;(2)17
【解析】试题分析:(1)如图2中,延长BD交OA于G,交AC于E.只要证明△AOC≌△BOD即可解决问题.
(2)如图3中,在![]() △ABC中,利用勾股定理求出
△ABC中,利用勾股定理求出![]() ,再根据
,再根据![]() 即可解决问题.
即可解决问题.
试题解析:(1)证明:如图2中,延长BD交OA于G,交AC于E.
∵∠AOB=∠COD=![]() ,
,
∴∠AOC=∠DOB,
在△AOC和△BOD中,

∴△AOC≌△BOD,
∴AC=BD,∠CAO=∠DBO,
∵∠DBO+∠GOB=![]() ,
,
∵∠OGB=∠AGE,
∴∠CAO+∠AGE=![]() ,
,
∴∠AEG=![]() ,
,
∴BD⊥AC.
(2)如图3中, ![]() △AOC≌△BOD,
△AOC≌△BOD,
![]()
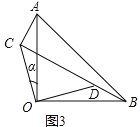
∵BD、CD在同一直线上,BD⊥AC,
∴△ABC是直角三角形,
∴![]()
![]()
解得![]()
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1:y1=﹣
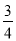 x+m与y轴交于点A(0,6),直线l2:y=kx+1分别与x轴交于点B(﹣2,0),与y轴交于点C,两条直线交点记为D.
x+m与y轴交于点A(0,6),直线l2:y=kx+1分别与x轴交于点B(﹣2,0),与y轴交于点C,两条直线交点记为D.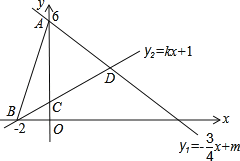
(1)m= ,k= ;
(2)求两直线交点D的坐标;
(3)根据图象直接写出y1<y2时自变量x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,D为AC上一点,DE⊥AB于点E,AC=12,BC=5.
(1)求cos∠ADE的值;
(2)当DE=DC时,求AD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,双曲线y=
 与直线y=kx﹣2交于点A(3,1).
与直线y=kx﹣2交于点A(3,1).
(1)求直线和双曲线的解析式;
(2)直线y=kx﹣2与x轴交于点B,点P是双曲线y= 上一点,过点P作直线PC∥x轴,交y轴于点C,交直线y=kx﹣2于点D.若DC=2OB,写出点P的坐标.
上一点,过点P作直线PC∥x轴,交y轴于点C,交直线y=kx﹣2于点D.若DC=2OB,写出点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,过点B作⊙O的切线DE,F为射线BD上一点,连接CF.
(1)求证:∠CBE=∠A;
(2)若⊙O的直径为5,BF=2,tanA=2,求CF的长.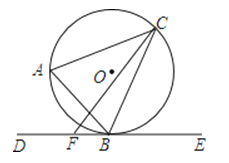
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC是等腰直角三角形,AB=
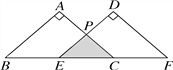
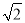 ,把△ABC沿直线BC向右平移得到△DEF.如果E是BC的中点,AC与DE交于P点,以直线BC为x轴,点E为原点建立直角坐标系.
,把△ABC沿直线BC向右平移得到△DEF.如果E是BC的中点,AC与DE交于P点,以直线BC为x轴,点E为原点建立直角坐标系.(1)求△ABC与△DEF的顶点坐标;
(2)判断△PEC的形状;
(3)求△PEC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)阅读并回答:
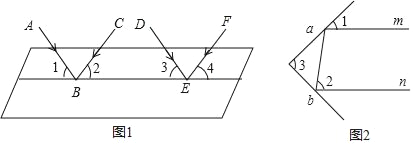
科学实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的角相等.如图1,一束平行光线AB与DE射向一个水平镜面后被反射,此时∠1=∠2,∠3=∠4.
由条件可知:∠1与∠3的大小关系是 ,理由是 ;∠2与∠4的大小关系是 ;
反射光线BC与EF的位置关系是 ,理由是 ;
(2)解决问题:
①如图2,一束光线m射到平面镜a上,被a反射到平面镜b上,又被b镜反射,若b反射出的光线n平行于m,且∠1=35°,则∠2= ,∠3= ;
在①中,若∠1=40°,则∠3= ,
由①②请你猜想:当∠3= 时,任何射到平面镜a上的光线m经过平面镜a和b的两次反射后,入射光线m与反射光线n总是平行的?请说明理由.
相关试题

