【题目】数学活动课上，老师提出问题：如图，有一张长4dm，宽3dm的长方形纸板，在纸板的四个角裁去四个相同的小正方形，然后把四边折起来，做成一个无盖的盒子，问小正方形的边长为多少时，盒子的体积最大．

下面是探究过程，请补充完整：

（1）设小正方形的边长为xdm，体积为ydm3，根据长方体的体积公式得到y和x的关系式：　　；

（2）确定自变量x的取值范围是　　；

（3）列出y与x的几组对应值．

x/dm

…

1

…

y/dm3

…

1.3

2.2

2.7

3.0

2.8

2.5

1.5

0.9

…

（说明：表格中相关数值保留一位小数）

（4）在下面的平面直角坐标系xOy中，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；

（5）结合画出的函数图象，解决问题：当小正方形的边长约为　　dm时，盒子的体积最大，最大值约为　　dm3．

参考答案：

【答案】(1) y= 4x3﹣14x2+12x;(2) 0＜x＜; (3)见解析；(4)见解析;(5) 0.55，3.03.

【解析】

根据题意，列出y与x的函数关系式，根据盒子长宽高值为正数，求出自变量取值范围；利用图象求出盒子最大体积．

（1）由已知，y=x（4-2x）（3-2x）=4x3-14x2+12x，

故答案为：y=4x3-14x2+12x，

（2）由已，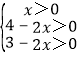

解得：0＜x＜，

（3）根据函数关系式，当x=时，y=3；x=1时，y=2，

（4）根据（1）画出函数图象如图，

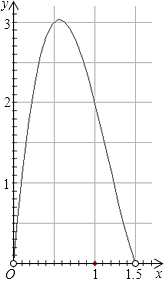
（5）根据图象，当x=0.55dm时，盒子的体积最大，最大值约为3.03dm3.

故答案为：0.55，3.03.

关闭