【题目】如图,在△ABC中,∠ACB=120°,BC=4,D为AB的中点,DC⊥BC,则△ABC的面积是___.

参考答案:
【答案】8![]() .
.
【解析】
根据垂直的定义得到∠BCD=90°,延长CD到H使DH=CD,由线段中点的定义得到AD=BD,根据全等三角形的性质得到AH=BC=4,∠H=∠BCD=90°,求得CD=2![]() ,于是得到结论.
,于是得到结论.
解:∵DC⊥BC,
∴∠BCD=90°,
∵∠ACB=120°,
∴∠ACD=30°,
延长CD到H使DH=CD,
∵D为AB的中点,
∴AD=BD,
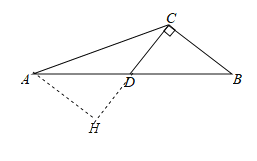
在△ADH与△BCD中,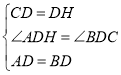 ,
,
∴△ADH≌△BCD(SAS),
∴AH=BC=4,∠H=∠BCD=90°,
∵∠ACH=30°,
∴CH=![]() AH=4
AH=4![]() ,
,
∴CD=2![]() ,
,
∴△ABC的面积=2S△BCD=2×![]() ×4×2
×4×2![]() =8
=8![]() ,
,
故答案为:8![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)在图中作出△ABC关于直线m对称的△A′B′C′,并写出A′、B′、C′三点的坐标(2)猜想:坐标平面内任意点P(x,y)关于直线m对称点P′的坐标为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】数学活动课上,老师提出问题:如图,有一张长4dm,宽3dm的长方形纸板,在纸板的四个角裁去四个相同的小正方形,然后把四边折起来,做成一个无盖的盒子,问小正方形的边长为多少时,盒子的体积最大.
下面是探究过程,请补充完整:
(1)设小正方形的边长为xdm,体积为ydm3,根据长方体的体积公式得到y和x的关系式: ;
(2)确定自变量x的取值范围是 ;
(3)列出y与x的几组对应值.
x/dm
…







1


…
y/dm3
…
1.3
2.2
2.7
3.0
2.8
2.5
1.5
0.9
…
(说明:表格中相关数值保留一位小数)
(4)在下面的平面直角坐标系xOy中,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
(5)结合画出的函数图象,解决问题:当小正方形的边长约为 dm时,盒子的体积最大,最大值约为 dm3.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,二次函数y=x2﹣2hx+h的图象的顶点为点D.
(1)当h=﹣1时,求点D的坐标;
(2)当﹣1≤x≤1时,求函数的最小值m.(用含h的代数式表示m)

-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,两组对边分别平行的四边形叫做平行四边形。平行四边形的内角和、外角和都等于360°,根据三角形的学习经验,请你再写出平行四边形的两条性质;并证明其中一条性质
(1)______________________________________________
(2)________________________________________________

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,点E是BC边上的一个动点,连接AE,将线段AE绕点A逆时针旋转90°,得到AF,连接EF,交对角线BD于点G,连接AG.
(1)根据题意补全图形;
(2)判定AG与EF的位置关系并证明;
(3)当AB=3,BE=2时,求线段BG的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,将任意两点P(x1,y1)与Q(x2,y2)之间的“直距”定义为:DPQ=|x1﹣x2|+|y1﹣y2|.
例如:点M(1,﹣2),点N(3,﹣5),则DMN=|1﹣3|+|﹣2﹣(﹣5)|=5.已知点A(1,0)、点B(﹣1,4).
(1)则DAO= ,DBO= ;
(2)如果直线AB上存在点C,使得DCO为2,请你求出点C的坐标;
(3)如果⊙B的半径为3,点E为⊙B上一点,请你直接写出DEO的取值范围.

相关试题

