【题目】(1)在图中作出△ABC关于直线m对称的△A′B′C′,并写出A′、B′、C′三点的坐标(2)猜想:坐标平面内任意点P(x,y)关于直线m对称点P′的坐标为 .

参考答案:
【答案】⑴见解析;A′(5,5), B′(6,2), C′(4,1); ⑵ P′(2-x, y)
【解析】
(1)直接利用关于直线对称点的性质得出对应点位置进而得出答案;
(2)利用对称轴为直线m=1,进而得出P′点坐标.
(1)如图所示:△A′B′C′,即为所求, A′(5,5), B′(6,2), C′(4,1);

(2)∵△ABC的内部一点P(x,y),
设点P关于直线m对称的点P′的横坐标为:a,
则![]() =1,故a=2x,
=1,故a=2x,
∴点P关于直线m对称的点P′的坐标是(2x,y).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABD和△ACE分别是等边三角形,AB≠AC,下列结论中正确有( )个.

⑴DC=BE,⑵∠BOD=60°,⑶∠BDO=∠CEO,⑷AO平分∠DOE,⑸AO平分∠BAC
A. 2 B. 3 C. 4 D. 5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2+bx+c交x轴于点A(﹣3,0)和点B,交y轴于点C(0,3).
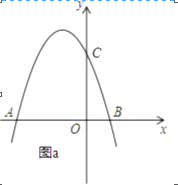
(1)求抛物线的函数表达式;
(2)若点P在抛物线上,且S△AOP=4SBOC , 求点P的坐标;
(3)如图b,设点Q是线段AC上的一动点,作DQ⊥x轴,交抛物线于点D,求线段DQ长度的最大值.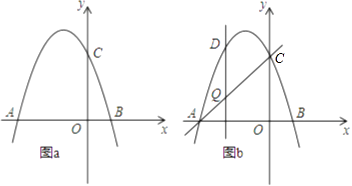
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠MON=30°,点B1、B2、B3…和A1、A2、A3…分别在OM和ON上,且△A1B1A2、△A2B2A3、△A3B3A4、…分别为等边三角形,已知OA1=1,则△A2018B2018A2019的边长为_____.
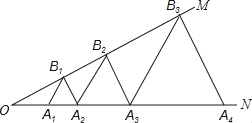
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,△ABD和△ACE分别是以AB、AC为斜边的等腰直角三角形,BE、CD相交于点F.求证:AF⊥BC.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如∠MON=30°、OP=6,点A、B分别在OM、ON上;(1)请在图中画出周长最小的△PAB(保留画图痕迹);(2)请求出(1)中△PAB的周长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=900,∠B=∠E=300.
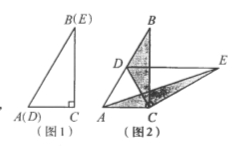


(1)操作发现如图2,固定△ABC,使△DEC绕点C旋转。当点D恰好落在BC边上时,填空:线段DE与AC的位置关系是 ;
② 设△BDC的面积为S1,△AEC的面积为S2。则S1与S2的数量关系是 。
(2)猜想论证
当△DEC绕点C旋转到图3所示的位置时,小明猜想(1)中S1与S2的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC,CE边上的高,请你证明小明的猜想。
(3)拓展探究
已知∠ABC=600,点D是其角平分线上一点,BD=CD=4,OE∥AB交BC于点E(如图4),若在射线BA上存在点F,使S△DCF =S△BDC,请直接写出相应的BF的长
相关试题

