【题目】如图,在等边△ABC中,点D在BC边上,点E在AC的延长线上,DE=DA.
(1)求证:∠BAD=∠EDC;
(2)作出点E关于直线BC的对称点M,连接DM、AM,猜想DM与AM的数量关系,并说明理由.

参考答案:
【答案】(1)见解析;(2) 猜想:DM=AM. 理由见解析.
【解析】
(1)根据等边三角形的性质得出相等的角,相等的边,再等量代换即可得证;
(2)根据题意画出图形,根据轴对称的性质,得∠MDC=∠EDC,DE=DM,然后根据(1)的结论和等边三角形的性质证明即可.
(1)证明:∵△ABC是等边三角形,∴∠BAC=∠ACB=60°.
又∵∠BAD+∠DAC=∠BAC,∠EDC+∠DEC=∠ACB,
∴∠BAD+∠DAC=∠EDC+∠DEC.
∵DE=DA,∴∠DAC=∠DEC,
∴∠BAD=∠EDC.
(2)解:按题意画图如图所示.

猜想:DM=AM.
理由如下:∵点M、E关于直线BC对称,
∴∠MDC=∠EDC,DE=DM.
又由(1)知∠BAD=∠EDC,∴∠MDC=∠BAD.
∵∠ADC=∠BAD+∠B,即∠ADM+∠MDC=∠BAD+∠B,
∴∠ADM=∠B=60°.
又∵DA=DE=DM,
∴△ADM是等边三角形,
∴DM=AM.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知数轴上有三点A、B、C,AB=60,点A对应的数是40.

(1)若
 ,求点C到原点的距离;
,求点C到原点的距离;(2)如图2,在(1)的条件下,动点P、Q两点同时从C、A出发向右运动,同时动点R从点A向左运动,已知点P的速度是点R的速度的3倍,点Q的速度是点R的速度2倍少5个单位长度/秒.经过5秒,点P、Q之间的距离与点Q、R之间的距离相等,求动点Q的速度;
(3)如图3,在(1)的条件下,O表示原点,动点P、T分别从C、O两点同时出发向左运动,同时动点R从点A出发向右运动,点P、T、R的速度分别为5个单位长度/秒、1个单位长度/秒、2个单位长度/秒,在运动过程中,如果点M为线段PT的中点,点N为线段OR的中点.请问
 的值是否会发生变化?若不变,请求出相应的数值;若变化,请说明理由.
的值是否会发生变化?若不变,请求出相应的数值;若变化,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】按下列程序计算,把答案填写在表格内,然后观察有什么规律,想一想:为什么会有这个规律?
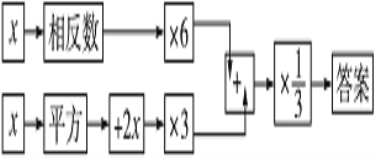
(1)填写表内空格:
输入
-3
-2
-1
0
…
输出答案
9
…
(2)发现的规律是:输入数据x,则输出的答案是__________;
(3)为什么会有这个规律?请你说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年3月12日植树节活动中,某单位的职工分成两个小组植树,已知他们植树的总数相同,均为100多棵,如果两个小组人数不等,第一组有一人植了6棵,其他每人都植了13棵;第二组有一人植了5棵,其他每人都植了10棵,则该单位共有职工人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
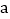 、
、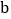 、
、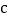 在数轴上的位置如图所示,所对应的点分别为
在数轴上的位置如图所示,所对应的点分别为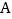 、
、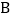 、
、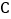 ,
,
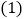 在数轴上表示
在数轴上表示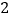 的点与表示
的点与表示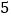 的点之间的距离为________;
的点之间的距离为________;在数轴上表示
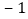 的点与表示
的点与表示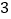 的点之间的距离为________;
的点之间的距离为________;在数轴上表示
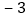 的点与表示
的点与表示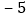 的点之间的距离为________;
的点之间的距离为________;由此可得点
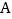 、
、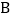 之间的距离为________,点
之间的距离为________,点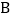 、
、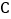 之间的距离为________,点
之间的距离为________,点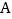 、
、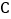 之间的距离为________
之间的距离为________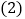 化简:
化简: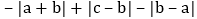 ;
; 若
若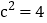 ,
,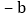 的倒数是它本身,
的倒数是它本身,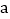 的绝对值的相反数是
的绝对值的相反数是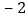 ,
,求
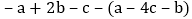 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1 , 连接AD1、BC1 . 若∠ACB=30°,AB=1,CC1=x,△ACD与△A1C1D1重叠部分面积为S,则下列结论:
①△A1AD1≌△CC1B;
②当x=1时,四边形ABC1D1是菱形;
③当x=2时,△BDD1为等边三角形;
④S= (x﹣2)2(0≤x≤2).
(x﹣2)2(0≤x≤2).
其中正确的是(将所有正确答案的序号都填写在横线上)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列方程中变形正确的是( )
①3x+6=0变形为x+2=0;
②2x+8=5-3x变形为x=3;
③
 +
+ =4去分母,得3x+2x=24;
=4去分母,得3x+2x=24;④(x+2)-2(x-1)=0去括号,得x+2-2x-2=0.
A. ①③ B. ①②③ C. ①④ D. ①③④
相关试题

