搜索
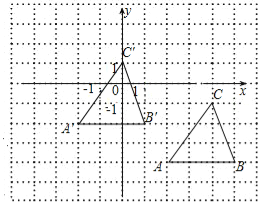
【题目】如图，方格纸中每个小方格都是边长为1个单位长度的正方形，在建立平面直角坐标系后，⊿ABC的顶点在格点上。 且A（1，-4），B（5，-4），C（4，-1）
【1】画出⊿ABC；
【1】求出⊿ABC 的面积；
【1】若把⊿ABC向上平移2个单位长度，再向左平移4个单位长度得到⊿
B
C
，在图中画出⊿
B
C
，并写出B的坐标。
参考答案：
【答案】
【1】作图略
【1】⊿ABC的面积=
ⅹ4ⅹ3=6
【1】点B’（1，-2）
【解析】
【1】根据各象限内点的符号和距坐标轴的距离可得坐标系中A、B、C三点，顺次连接三点即为△ABC；
【1】△ABC的面积等于底边4×高3÷2；
【1】把△ABC各点向上平移2个单位长度，再向左平移4个单位长度，再顺次连接平移后的各点即为平移后的△A′B′C′，根据各象限内点的符号和距坐标轴的距离可得B′的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）如图①在△ABC中，点D是BC边上的一点，将△ABD沿AD折叠，得到△AED，AE与BC交于点F．已知∠B＝50°，∠BAD＝15°，求∠AFC的度数．
（2）如图②，将△ABC纸片沿DE折叠，使点A落在四边形BCED的内部点A′的位置，∠1、∠2与∠A之间存在一定的数量关系，请判断它们之间的关系，并说明理由．
（3）如图③，将△ABC纸片沿DE折叠，使点A落在四边形BCED的外部点A′的位置，此时∠1、∠2与∠A之间也存在一定的数量关系，请直接写出它们之间的关系，无需说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】八年级一班开展了“读一本好书”的活动，班委会对学生阅读书籍的情况进行了问卷调查，问卷设置了“小说”、“戏剧”、“散文”、“其他”
四个类别，每位同学仅选一项，根据调查结果绘制了不完整的频数分布表和扇形统计图．根据图表提供的信息，回答下列问题：类别
频数（人数）
频率
小说
0.5
戏剧
4
散文
10
0.25
其他
6
合计
m
1
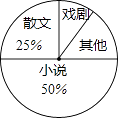
（1）计算m=；
（2）在扇形统计图中，“其他”类所占的百分比为；
（3）在调查问卷中，甲、乙、丙、丁四位同学选择了“戏剧”类，现从中任意选出2名同学参加学校的戏剧社团，请用画树状图或列表的方法，求选取的2人恰好是乙和丙的概率． -
科目： 来源： 题型：
查看答案和解析>>【题目】红星中学计划组织“春季研修活动，活动组织负责人从公交公司了解到如下租车信息：
车型
载客量（人/辆）
租金（元/辆）
校方从实际情况出发,决定租用
、型客车共
辆，而且租车费用不超过
元。（1）请为校方设计可能的租车方案；
（2）在（1）的条件下，校方根据自愿的原则，统计发现有
人参加，请问校方应如何租车，且又省钱? -
科目： 来源： 题型：
查看答案和解析>>【题目】7张如图1的长为a，宽为b（a＞b）的小长方形纸片，按图2的方式不重叠地放在矩形ABCD内，未被覆盖的部分（两个矩形）用阴影表示．设左上角与右下角的阴影部分的面积的差为S，当BC的长度变化时，按照同样的放置方式，S始终保持不变，则a，b满足（ ）
A.a=
bB.a=3bC.a=
bD.a=4b -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在ABCD中，∠ABD的平分线BE交AD于点E，∠CDB的平分线DF交BC于点F．
（1）求证：△ABE≌△CDF；
（2）若AB=DB，猜想：四边形DFBE是什么特殊的四边形？并说明理由． -
科目： 来源： 题型：
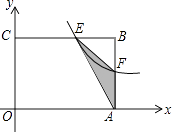
查看答案和解析>>【题目】如图，在矩形OABC中，OA=3，OC=2，F是AB上的一个动点（F不与A，B重合），过点F的反比例函数y=kx﹣1（k＞0）的图象与BC边交于点E．当F为AB的中点时，求该函数的解析式．
相关试题
