【题目】甲、乙两个电子厂在广告中都声称他们的某种电子产品在正常情况下的使用寿命都是5年.质检部门对这两家销售的产品的使用寿命进行了跟踪调查,统计结果如下:(单位:年)
甲厂:3,4,5,6,7 乙厂:4,4,5,6,6
(1)分别求出甲、乙两厂的该种电子产品在正常情况下的使用寿命的平均数和方差;
(2)如果你是顾客,你会选购哪家电子厂的产品?说明理由.
参考答案:
【答案】(1)见解析(2)选乙厂的产品
【解析】试题分析:(1)平均数就是把这组数据加起来的和除以这组数据的总数,再利用方差公式求出即可;
(2)由(1)的结果容易回答,甲厂、乙厂分别利用了平均数、方差进行广告推销,顾客在选购产品时,一般平均数相同,根据方差的大小进行选择.
试题解析:
(1)x甲=![]() ×(3+4+5+6+7)=5,
×(3+4+5+6+7)=5,
![]() 甲=
甲=![]() ×[(3-5)2+(4-5)2+(5-5)2+(6-5)2+(7-5)2]=2,
×[(3-5)2+(4-5)2+(5-5)2+(6-5)2+(7-5)2]=2,
x乙=![]() ×(4+4+5+6+6)=5,
×(4+4+5+6+6)=5,
![]() 乙=
乙=![]() ×[(4-5)2+(4-5)2+(5-5)2+(6-5)2+(6-5)2]=0.8.
×[(4-5)2+(4-5)2+(5-5)2+(6-5)2+(6-5)2]=0.8.
(2)由(1)知,甲厂、乙厂的该种电子产品在正常情况下的使用寿命平均数都是5年,
则甲厂方差>乙厂方差,选方差小的厂家的产品,
因此应选乙厂的产品.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=
 x2+bx+c经过△ABC的三个顶点,其中点A(0,1),B(9,10),AC∥x轴,点P是直线AC下方抛物线上的动点。
x2+bx+c经过△ABC的三个顶点,其中点A(0,1),B(9,10),AC∥x轴,点P是直线AC下方抛物线上的动点。(1)求抛物线的解析式;
(2)过点P且与y轴平行的直线l与直线AB、AC分别交于点E.F,当四边形AECP的面积最大时,求点P的坐标和四边形AECP的最大面积;
(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C.P、Q为顶点的三角形与△ABC相似?若存在,求出点Q的坐标;若不存在,请说明理由。

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=x2-2x-3,点P在该函数的图象上,点P到x轴、y轴的距离分别为d1、d2.设d=d1+d2,下列结论中: ①d没有最大值; ②d没有最小值; ③ -1<x<3时,d 随x的增大而增大; ④满足d=5的点P有四个.其中正确结论的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠ABC、∠ACB的平分线BD,CE相交于O点,且BD交AC于点D,CE交AB于点E,某同学分析图形后得出以下结论,上述结论一定正确的是______(填代号).
①△BCD≌△CBE;②△BAD≌△BCD;③△BDA≌△CEA;④△BOE≌△COD;⑤△ACE≌△BCE.

-
科目: 来源: 题型:
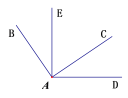
查看答案和解析>>【题目】如图所示,已知∠BAC=∠EAD=90o.
(1)判断∠BAE与∠CAD的大小关系,并说明理由.
(2)当∠EAC=60o时,求∠BAD的大小.
(3)探究∠EAC与∠BAD的数量关系,请直接写出结果,不要求说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上),已知AB=80 m,DE=10 m,求障碍物B,C两点间的距离.(结果精确到0.1 m)(参考数据:
 ≈1.414,、
≈1.414,、 ≈1.732)
≈1.732)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,O为坐标原点,矩形OABC中,A(10,0),C(0,4),D为OA的中点,P为BC边上一点.若△POD为等腰三角形,则所有满足条件的点P的坐标为 .

相关试题

