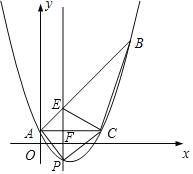
【题目】如图,已知抛物线y=![]() x2+bx+c经过△ABC的三个顶点,其中点A(0,1),B(9,10),AC∥x轴,点P是直线AC下方抛物线上的动点。
x2+bx+c经过△ABC的三个顶点,其中点A(0,1),B(9,10),AC∥x轴,点P是直线AC下方抛物线上的动点。
(1)求抛物线的解析式;
(2)过点P且与y轴平行的直线l与直线AB、AC分别交于点E.F,当四边形AECP的面积最大时,求点P的坐标和四边形AECP的最大面积;
(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C.P、Q为顶点的三角形与△ABC相似?若存在,求出点Q的坐标;若不存在,请说明理由。

参考答案:
【答案】(1) y= ![]() x2x+1;(2) 四边形AECP的面积最大值是
x2x+1;(2) 四边形AECP的面积最大值是![]() ,此时P(
,此时P(![]() ,
,![]() );
);
(3) Q点的坐标为(4,1)或(3,1),理由见解析.
【解析】分析:(1)把点A,B的坐标代入抛物线的解析式中,求b,c;(2)设P(m,![]() m22m+1),根据S四边形AECP=S△AEC+S△APC,把S四边形AECP用含m式子表示,根据二次函数的性质求解;(3)设Q(t,1),分别求出点A,B,C,P的坐标,求出AB,BC,CA;用含t的式子表示出PQ,CQ,判断出∠BAC=∠PCA=45°,则要分两种情况讨论,根据相似三角形的对应边成比例求t.
m22m+1),根据S四边形AECP=S△AEC+S△APC,把S四边形AECP用含m式子表示,根据二次函数的性质求解;(3)设Q(t,1),分别求出点A,B,C,P的坐标,求出AB,BC,CA;用含t的式子表示出PQ,CQ,判断出∠BAC=∠PCA=45°,则要分两种情况讨论,根据相似三角形的对应边成比例求t.
详解:(1)将A(0,1),B(9,10)代入函数解析式得:
![]() ×81+9b+c=10,c=1,解得b=2c=1,
×81+9b+c=10,c=1,解得b=2c=1,
所以抛物线的解析式y=![]() x22x+1;
x22x+1;
(2)∵AC∥x轴,A(0,1),
∴![]() x22x+1=1,解得x1=6,x2=0(舍),即C点坐标为(6,1),
x22x+1=1,解得x1=6,x2=0(舍),即C点坐标为(6,1),
∵点A(0,1),点B(9,10),
∴直线AB的解析式为y=x+1,设P(m,![]() m22m+1),∴E(m,m+1),
m22m+1),∴E(m,m+1),
∴PE=m+1(![]() m22m+1)=
m22m+1)=![]() m2+3m.
m2+3m.
∵AC⊥PE,AC=6,
∴S四边形AECP=S△AEC+S△APC=![]() ACEF+
ACEF+![]() ACPF
ACPF
=![]() AC(EF+PF)=
AC(EF+PF)=![]() ACEP
ACEP
=![]() ×6(
×6(![]() m2+3m)=m2+9m.
m2+3m)=m2+9m.
∵0<m<6,
∴当m=![]() 时,四边形AECP的面积最大值是
时,四边形AECP的面积最大值是![]() ,此时P(
,此时P(![]() );
);
(3)∵y=![]() x22x+1=
x22x+1=![]() (x3)22,
(x3)22,
P(3,2),PF=yFyp=3,CF=xFxC=3,
∴PF=CF,∴∠PCF=45,
同理可得∠EAF=45,∴∠PCF=∠EAF,
∴在直线AC上存在满足条件的点Q,
设Q(t,1)且AB=![]() ,AC=6,CP=
,AC=6,CP=![]() ,
,
∵以C,P,Q为顶点的三角形与△ABC相似,
①当△CPQ∽△ABC时,
CQ:AC=CP:AB,(6t):6=![]() ,解得t=4,所以Q(4,1);
,解得t=4,所以Q(4,1);
②当△CQP∽△ABC时,
CQ:AB=CP:AC,(6t)![]() 6,解得t=3,所以Q(3,1).
6,解得t=3,所以Q(3,1).
综上所述:当点P为抛物线的顶点时,在直线AC上存在点Q,使得以C,P,Q为顶点的三角形与△ABC相似,Q点的坐标为(4,1)或(3,1).
-
科目: 来源: 题型:
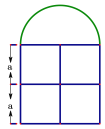
查看答案和解析>>【题目】窗户的形状如图所示(图中长度单位:cm),其中上部是半圆形,下部是边长相同的四个小正方形. 已知下部小正方形的边长是acm.
(1)计算窗户的面积(计算结果保留π).
(2)计算窗户的外框的总长(计算结果保留π).
(3)安装一种普通合金材料的窗户单价是175元/平方米,当a=50cm时,请你帮助计算这个窗户安装这种材料的费用(π≈3.14,窗户面积精确到0.1).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ABC为等腰直角三角形,∠ACB=90,F是AC边上的一个动点(点F与A. C不重合),以CF为一边在等腰直角三角形外作正方形CDEF,连接BF、AD.
(1)猜想图1中线段BF、AD的数量关系及所在直线的位置关系,直接写出结论;
(2)将图1中的正方形CDEF,绕着点C按顺时针方向旋转任意角度α,得到如图2的情形。图2中BF交AC于点H,交AD于点O,请你判断(1)中得到的结论是否仍然成立,并证明你的判断。
(3)将原题中的等腰直角三角形ABC改为直角三角形ABC,∠ACB=90,正方形CDEF改为矩形CDEF,如图3,且AC=4,BC=3,CD=
 ,CF=1,BF交AC于点H,交AD于点O,连接BD、AF,求BD2+AF2的值。
,CF=1,BF交AC于点H,交AD于点O,连接BD、AF,求BD2+AF2的值。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AD平分∠BAC,DE∥AC交AB于E,DF∥AB交AC于F,若AF=6,则四边形AEDF的周长是( )

A. 24 B. 28 C. 32 D. 36
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=x2-2x-3,点P在该函数的图象上,点P到x轴、y轴的距离分别为d1、d2.设d=d1+d2,下列结论中: ①d没有最大值; ②d没有最小值; ③ -1<x<3时,d 随x的增大而增大; ④满足d=5的点P有四个.其中正确结论的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠ABC、∠ACB的平分线BD,CE相交于O点,且BD交AC于点D,CE交AB于点E,某同学分析图形后得出以下结论,上述结论一定正确的是______(填代号).
①△BCD≌△CBE;②△BAD≌△BCD;③△BDA≌△CEA;④△BOE≌△COD;⑤△ACE≌△BCE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两个电子厂在广告中都声称他们的某种电子产品在正常情况下的使用寿命都是5年.质检部门对这两家销售的产品的使用寿命进行了跟踪调查,统计结果如下:(单位:年)
甲厂:3,4,5,6,7 乙厂:4,4,5,6,6
(1)分别求出甲、乙两厂的该种电子产品在正常情况下的使用寿命的平均数和方差;
(2)如果你是顾客,你会选购哪家电子厂的产品?说明理由.
相关试题

