【题目】已知关于x的一元二次方程ax2﹣2x﹣1=0有两个不相等的实数根,则a的取值范围是 .
参考答案:
【答案】a>﹣1且a≠0
【解析】解:根据题意得a≠0且△=(﹣2)2﹣4a(﹣1)>0, 解得a>﹣1且a≠0.
所以答案是a>﹣1且a≠0.
【考点精析】掌握求根公式是解答本题的根本,需要知道根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:a,b互为相反数,c,d互为倒数,x的绝对值是2,求:(a+b+cd)x+(a+b)2017+(﹣cd)2018的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用一个平面去截一个几何体,截面形状为四边形,则这个几何体不可能为( )
A. 立方体 B. 圆柱 C. 圆锥 D. 三棱柱
-
科目: 来源: 题型:
查看答案和解析>>【题目】若|﹣x|=2.4,则x= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,点D,E在AB上,且AF垂直平分CD,BG垂直平分CE.(1)求∠ECD的度数;(2)若∠ACB为α,则∠ECD的度数能否用含α的式子来表示.
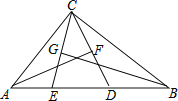
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CE、CB分别是△ABC与△ADC的中线,且∠ACB=∠ABC.求证:CD=2CE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:△ABC中,∠ACB=90°,∠CAD=30°,AC=BC=AD,CE⊥CD,且CE=CD,连接BD,DE,BE,则下列结论:①∠ECA=165°,②BE=BC;③AD⊥BE;其中正确的是_________
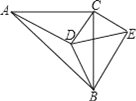
相关试题

