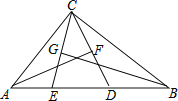
【题目】如图,在△ABC中,∠ACB=90°,点D,E在AB上,且AF垂直平分CD,BG垂直平分CE.(1)求∠ECD的度数;(2)若∠ACB为α,则∠ECD的度数能否用含α的式子来表示.
参考答案:
【答案】见解析
【解析】试题分析:
(1)由AF垂直平分CD可得AC=AD,再由等腰三角形的“三线合一”可得∠FAB=![]() ∠CAB,同理可得∠GBA=
∠CAB,同理可得∠GBA=![]() ∠CBA;如图,设AF、BG相交于点O,则∠GOF=∠AOB=180°-∠FAB-∠GBA=180°-
∠CBA;如图,设AF、BG相交于点O,则∠GOF=∠AOB=180°-∠FAB-∠GBA=180°-![]() (180°-∠ACB)=135°,由此在四边形GOFC中可得∠ECD=360°-∠CGO-∠CFO-∠GOF=360°-90°-90°-∠GOF=180°-135°=45°.
(180°-∠ACB)=135°,由此在四边形GOFC中可得∠ECD=360°-∠CGO-∠CFO-∠GOF=360°-90°-90°-∠GOF=180°-135°=45°.
(2)思路同(1)只需把∠ACB=90°换成∠ACB= ![]() 可解得∠DCE=90°-
可解得∠DCE=90°- ![]() .
.

试题解析:
(1)如图,设AF、BG相交于点O,连接CO,
∵AF垂直平分CD,
∴AC=AD,∠CFO=90°,∴∠FAB=![]() ∠CAB.
∠CAB.
同理可得:∠CGO=90°,∠GBA=![]() ∠CBA.
∠CBA.
∴∠GOF=∠AOB=180°-∠FAB-∠GBA=180°-![]() (180°-∠ACB)=90°+
(180°-∠ACB)=90°+![]() ∠ACB=135°,
∠ACB=135°,
∵四边形GOFC的内角和为360°,
∴∠ECD=360°-∠CGO-∠CFO-∠GOF
=360°-90°-90°-∠GOF
=180°-135°
=45°.
(2)同(1)可得∠GOF=90°+![]() ∠ACB=90°+
∠ACB=90°+ ![]() ,∠CFO=90°,∠CGO=90°,
,∠CFO=90°,∠CGO=90°,
∵四边形GOFC的内角和为360°,
∴∠ECD=360°-∠CGO-∠CFO-∠GOF
=360°-90°-90°-∠GOF
=180°-(90°+ ![]() )
)
=90°- ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用一个平面去截一个几何体,截面形状为四边形,则这个几何体不可能为( )
A. 立方体 B. 圆柱 C. 圆锥 D. 三棱柱
-
科目: 来源: 题型:
查看答案和解析>>【题目】若|﹣x|=2.4,则x= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程ax2﹣2x﹣1=0有两个不相等的实数根,则a的取值范围是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CE、CB分别是△ABC与△ADC的中线,且∠ACB=∠ABC.求证:CD=2CE.

-
科目: 来源: 题型:
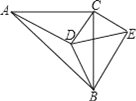
查看答案和解析>>【题目】如图:△ABC中,∠ACB=90°,∠CAD=30°,AC=BC=AD,CE⊥CD,且CE=CD,连接BD,DE,BE,则下列结论:①∠ECA=165°,②BE=BC;③AD⊥BE;其中正确的是_________
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,抛物线
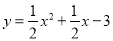 与x轴相交于A、B两点(点A在点B的右侧),已知C(0,
与x轴相交于A、B两点(点A在点B的右侧),已知C(0,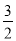 ).连接AC.
).连接AC.(1)求直线AC的解析式.
(2)点P是x轴下方的抛物线上一动点,过点P作PE⊥x轴交直线AC于点E,交x轴于点F,过点P作PG⊥AE于点G,线段PG交x轴于点H.设l=EP﹣
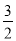 FH,求l的最大值.
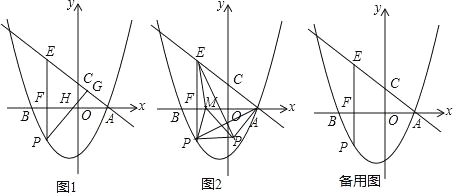
FH,求l的最大值.(3)如图2,在(2)的条件下,点M是x轴上一动点,连接EM、PM,将△EPM沿直线EM折叠为△EP1M,连接AP,AP1.当△APP1是等腰三角形时,试求出点M的坐标.
相关试题

