【题目】如图,Rt△ABC中,∠ACB=90°,AC边上的垂直平分线交AC于D,交AB于E,延长DE到F,使BF=CE
(1)四边形BCEF是平行四边形吗?说说你的理由.
(2)当∠A等于多少时,四边形BCEF是菱形,并说出你的理由.
(3)四边形BCEF可以是正方形吗?为什么?
参考答案:
【答案】
(1)解:四边形BCEF是平行四边形,理由如下:
证明:∵DF垂直且平分AC且∠ACB=90°
∴FD∥BC,AE=CE,
∴∠A=∠ACE,
∵∠A+∠ABC=∠ACE+∠BCE=90°,
∴∠ABC=∠BCE,
∴BE=CE=BF,
∴∠BFE=∠BEF
∵FD∥BC,
∴∠BFE=∠BEF=∠ABC=∠BCE
∴∠FBE=∠BEC,
∴FB∥EC,
∵CE=BF,
∴四边形BCEF为平行四边形;
(2)解:∠A=30°,
证明:∵∠A=30°,
∴∠ABC=60°且BE=CE,
∴△BCE为等边三角形,
∴BC=CE,
由(1)可知四边形BCEF为平行四边形,
∴四边形BCEF为菱形;
(3)解:不可以,
因为∠BCE始终是锐角,所以四边形BCEF不可能是正方形.
【解析】(1)根据已知,先证明FD∥BC得出∠BEF=∠ABC,再根据线段垂直平分线的性质推出∠A=∠ACE,根据等教的余角相等得出∠ABC=∠BCE,证得BE=CE=BF,得出∠BFE=∠BEF,然后证明FB∥EC,即可得出结论。
(2)四边形BCEF是平行四边形,要证明它是菱形,只需证明一组邻边相等,已征得BE=CE,若BC=CE,则BE=BC=CE,即得△BCE为等边三角形,因此∠A=30°。
(3)根据题意可知0°<∠BCE<90°,因此四边形BCEF不可能是正方形。
【考点精析】掌握线段垂直平分线的性质和平行四边形的判定是解答本题的根本,需要知道垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等;两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点B、E分别在直线AC和DF上,若∠AGB=∠EHF,∠C=∠D,可以证明
∠A=∠F.请完成下面证明过程中的各项“填空”
证明:∵∠AGB=∠EHF(已知)
∠AGB= (对顶角相等)
∴∠EHF=∠DGF(等量代换)
∴ ∥EC(理由: )
∴∠ =∠DBA(两直线平行,同位角相等)
又∵∠C=∠D,∴∠DBA= (等量代换)
∴DF∥ (内错角相等,两直线平行)
∴∠A=∠F(理由: )

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2+(2m﹣1)x+m2=0有两个实数根x1和x2 .
(1)求实数m的取值范围;
(2)当 时,求m的值.
时,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某高校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”,让同学们珍惜粮食,为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图.
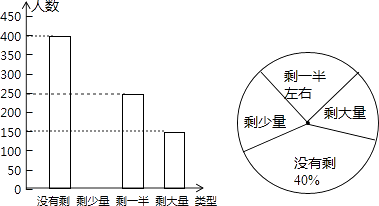
(1)这次被调查的同学共有名;
(2)把条形统计图补充完整;
(3)校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供200人用一餐.据此估算,该校18 000名学生一餐浪费的食物可供多少人食用一餐? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ACB和△ECD都是等腰直角三角形,CA=CB,CE=CD,△ACB的顶点A在△ECD的斜边DE上.
(1)求证:AE2+AD2=2AC2;
(2)如图2,若AE=3,AC=
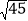 ,点F是AD的中点,求出CF的长.
,点F是AD的中点,求出CF的长.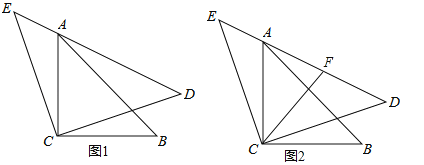
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图表示某公司“顺风车”与“快车”的行驶里程x(千米)与计费y(元)之间的函数图象.
(1)由图象写出乘车里程为5千米时选择 (“顺风车”或“快车”)更便宜;
(2)当x>5时,顺风车的函数是y=
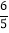 x+
x+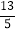 ,判断乘车,里程是8千米时,选择“顺风车”和“快车”哪个更便宜?说明理由.
,判断乘车,里程是8千米时,选择“顺风车”和“快车”哪个更便宜?说明理由.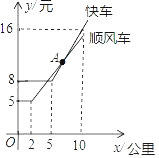
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,直线y=kx+1(k≠0)与双曲线y=
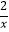 (x>0)相交于P(1,m).
(x>0)相交于P(1,m). 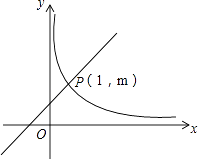
(1)求k的值;
(2)若点Q与点P关于y=x成轴对称,求点Q的坐标为
(3)若过P、Q两点的抛物线与y轴的交点为N(0, ),求该抛物线的解析式,并求出抛物线的对称轴方程.
),求该抛物线的解析式,并求出抛物线的对称轴方程.
相关试题

