【题目】如图,点B、E分别在直线AC和DF上,若∠AGB=∠EHF,∠C=∠D,可以证明
∠A=∠F.请完成下面证明过程中的各项“填空”
证明:∵∠AGB=∠EHF(已知)
∠AGB= (对顶角相等)
∴∠EHF=∠DGF(等量代换)
∴ ∥EC(理由: )
∴∠ =∠DBA(两直线平行,同位角相等)
又∵∠C=∠D,∴∠DBA= (等量代换)
∴DF∥ (内错角相等,两直线平行)
∴∠A=∠F(理由: )

参考答案:
【答案】∠DGF;BD;同位角相等,两直线平行;C;∠D;AC;两直线平行,内错角相等.
【解析】
先根据已知条件结合对顶角相等得出∠EHF=∠DGF,由平行线判定知BD∥EC,由判定得∠D=∠DBA,再由等量代换知∠DBA=∠C,根据平行线判定知DF∥AC,利用平行线的性质即可得证.
∵∠AGB=∠EHF(已知)
∠AGB=∠DGF(对顶角相等)
∴∠EHF=∠DGF(等量代换)
∴BD∥EC(理由:同位角相等,两直线平行)
∴∠D=∠DBA(两直线平行,同位角相等)
又∵∠C=∠D,∴∠DBA=∠C(等量代换)
∴DF∥AC(内错角相等,两直线平行)
∴∠A=∠F(理由:两直线平行,内错角相等).
故答案为:∠DGF;BD;同位角相等,两直线平行;C;∠D;AC;两直线平行,内错角相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场销售的一款空调机每台的标价是1635元,在一次促销活动中,按标价的八折销售,仍可盈利9%.
(1)求这款空调每台的进价(利润率= =
=  ).
).
(2)在这次促销活动中,商场销售了这款空调机100台,问盈利多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.求证:BF=2AE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形ABCD中,∠DAB=∠B=∠C=∠D=90°,AD=BC=16,AB=CD=34.点E为射线DC上的一个动点,△ADE与△AD′E关于直线AE对称,当△AD′B为直角三角形时,求DE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2+(2m﹣1)x+m2=0有两个实数根x1和x2 .
(1)求实数m的取值范围;
(2)当 时,求m的值.
时,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某高校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”,让同学们珍惜粮食,为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图.
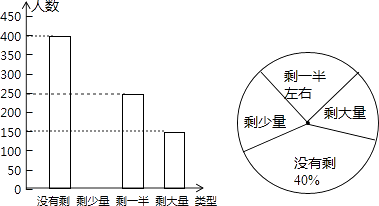
(1)这次被调查的同学共有名;
(2)把条形统计图补充完整;
(3)校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供200人用一餐.据此估算,该校18 000名学生一餐浪费的食物可供多少人食用一餐? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠ACB=90°,AC边上的垂直平分线交AC于D,交AB于E,延长DE到F,使BF=CE

(1)四边形BCEF是平行四边形吗?说说你的理由.
(2)当∠A等于多少时,四边形BCEF是菱形,并说出你的理由.
(3)四边形BCEF可以是正方形吗?为什么?
相关试题

