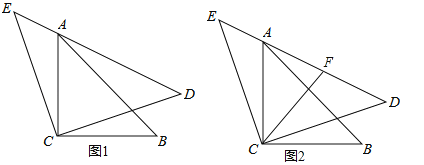
【题目】如图1,△ACB和△ECD都是等腰直角三角形,CA=CB,CE=CD,△ACB的顶点A在△ECD的斜边DE上.
(1)求证:AE2+AD2=2AC2;
(2)如图2,若AE=3,AC=![]() ,点F是AD的中点,求出CF的长.
,点F是AD的中点,求出CF的长.
参考答案:
【答案】(1)证明见解析;(2)![]()
【解析】
(1)连接BD,根据题意可以证明△ADB是直角三角形,然后根据三角形全等和勾股定理即可证明结论成立;
(2)过C作CM⊥ED于M.根据(1)中的结论得到AD的长,从而得到ED的长,根据等腰三角形的性质得到CM和MD的长,根据中点的性质及线段的和差得到MF的长.在Rt△CMF中,根据勾股定理即可得到结论.
(1)连接BD.
∵△ACB和△ECD都是等腰直角三角形,CA=CB,CE=CD,∴∠ECA+∠ACD=∠ACD+∠DCB=90°,∠CEA=∠CDE=45°,∠CAB=∠CBA=45°,∴∠ECA=∠DCB.
在△ECA和△DCB中,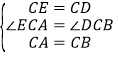 ,∴△ECA≌△DCB(SAS),∴AE=BD,∠CEA=∠CDB,∴∠ADB=∠CDB+∠EDC=90°,∴△ADB是直角三角形,∴AD2+BD2=AB2.
,∴△ECA≌△DCB(SAS),∴AE=BD,∠CEA=∠CDB,∴∠ADB=∠CDB+∠EDC=90°,∴△ADB是直角三角形,∴AD2+BD2=AB2.
在Rt△ACB中,AC=BC,AC2+BC2=2AC2=AB2,∴2AC2=AD2+BD2,即AE2+AD2=2AC2;
(2)过C作CM⊥ED于M.
∵AE2+AD2=2AC2,AE=3,AC=![]() ,∴AD=9,∴ED=EA+AD=3+9=12.
,∴AD=9,∴ED=EA+AD=3+9=12.
∵点F是AD的中点,∴AF=DF=4.5.
∵△ECD是等腰直角三角形,∴CM=![]() ED=MD=6,∴MF=MD-DF=6-4.5=1.5.在Rt△CMF中,CF=
ED=MD=6,∴MF=MD-DF=6-4.5=1.5.在Rt△CMF中,CF=![]() =
=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2+(2m﹣1)x+m2=0有两个实数根x1和x2 .
(1)求实数m的取值范围;
(2)当 时,求m的值.
时,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某高校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”,让同学们珍惜粮食,为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图.
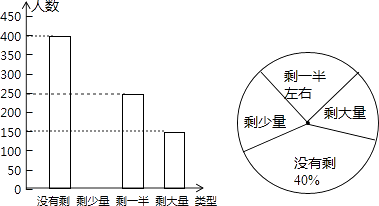
(1)这次被调查的同学共有名;
(2)把条形统计图补充完整;
(3)校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供200人用一餐.据此估算,该校18 000名学生一餐浪费的食物可供多少人食用一餐? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠ACB=90°,AC边上的垂直平分线交AC于D,交AB于E,延长DE到F,使BF=CE

(1)四边形BCEF是平行四边形吗?说说你的理由.
(2)当∠A等于多少时,四边形BCEF是菱形,并说出你的理由.
(3)四边形BCEF可以是正方形吗?为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图表示某公司“顺风车”与“快车”的行驶里程x(千米)与计费y(元)之间的函数图象.
(1)由图象写出乘车里程为5千米时选择 (“顺风车”或“快车”)更便宜;
(2)当x>5时,顺风车的函数是y=
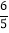 x+
x+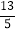 ,判断乘车,里程是8千米时,选择“顺风车”和“快车”哪个更便宜?说明理由.
,判断乘车,里程是8千米时,选择“顺风车”和“快车”哪个更便宜?说明理由.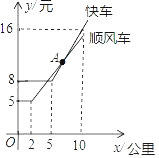
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,直线y=kx+1(k≠0)与双曲线y=
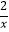 (x>0)相交于P(1,m).
(x>0)相交于P(1,m). 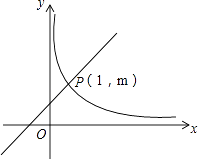
(1)求k的值;
(2)若点Q与点P关于y=x成轴对称,求点Q的坐标为
(3)若过P、Q两点的抛物线与y轴的交点为N(0, ),求该抛物线的解析式,并求出抛物线的对称轴方程.
),求该抛物线的解析式,并求出抛物线的对称轴方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,弦BD=BA,AB=12,BC=5,BE⊥DC交DC的延长线于点E.

(1)求证:∠BCA=∠BAD;
(2)求DE的长;
(3)求证:BE是⊙O的切线.
相关试题

