搜索
【题目】将下列各数填到相应的集合里：
-
，+5，-9，π，
，19, 1.2, 0，-5.26,0.8256…，5.3
正数集合﹛ …﹜
负数集合﹛ …﹜
整数集合﹛ …﹜
分数集合﹛ …﹜
有理数集合﹛ …﹜
参考答案：
【答案】+5， π，
，19, 1.2, 0.8256…，5.3；
-
， -9， -5.26；
+5，-9，19， 0；
-， ， 1.2, -5.26 ，5.3；
-，+5，-9，，19, 1.2, 0，-5.26，5.3.
【解析】
直接利用正数、负数、整数、分数以及有理数的定义分析得出答案．
解：正数集合﹛ +5， π，，19, 1.2, 0.8256…，5.3 …﹜
负数集合﹛ -， -9， -5.26, …﹜
整数集合﹛ +5，-9，19， 0， …﹜
分数集合﹛ -， ， 1.2, -5.26 ，5.3 ， …﹜
有理数集合﹛ -，+5，-9，，19, 1.2, 0，-5.26,5.3， …﹜
故答案为：+5， π，，19, 1.2, 0.8256…，5.3；-， -9， -5.26； +5，-9，19， 0；-， ， 1.2, -5.26 ，5.3；-，+5，-9，，19, 1.2, 0，-5.26，5.3.
-
科目： 来源： 题型：
查看答案和解析>>【题目】关于三角函数有如下公式：sin（α+β）=sinαcosβ+cosαsinβ，sin（α﹣β）=sinαcosβ﹣cosαsinβ
cos（α+β）=cosαcosβ﹣sinαsinβ，cos（α﹣β）=cosαcosβ+sinαsinβ
tan（α+β）=
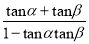（1﹣tanαtanβ≠0）tan（α﹣β）=
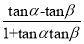（1+tanαtanβ≠0）利用这些公式可以将一些不是特殊角的三角函数转化为特殊角的三角函数来求值．
如：tan105°=tan（45°+60°）=
根据上面的知识，你可以选择适当的公式解决下面问题：
如图，两座建筑物AB和DC的水平距离BC为24米，从点A测得点D的俯角α=15°，测得点C的俯角β=75°，求建筑物CD的高度．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知正方形ABCD的对角线AC，BD相交于点O．
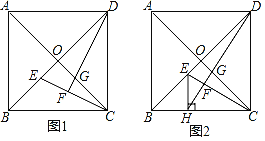
（1）如图1，E，G分别是OB，OC上的点，CE与DG的延长线相交于点F．若DF⊥CE，求证：OE=OG；
（2）如图2，H是BC上的点，过点H作EH⊥BC，交线段OB于点E，连结DH交CE于点F，交OC于点G．若OE=OG，
①求证：∠ODG=∠OCE；
②当AB=1时，求HC的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】对于一元二次方程
,下列说法:①若a+c=0,方程
有两个不等的实数根;②若方程有两个不等的实数根,则方程
也一定有两个不等的实数根;③若c是方程的一个根,则一定有
成立;④若m是方程的一个根,则一定有
成立.其中正确地只有 （ ）A. ①② B. ②③ C. ③④ D. ①④
-
科目： 来源： 题型：
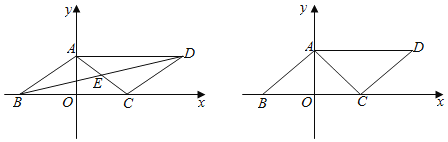
查看答案和解析>>【题目】如图，已知□ABCD边BC在x轴上，顶点A在y轴上，对角线AC所在的直线为y=
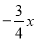+6，且AC=AB，若点P从点A出发以1cm/s的速度向终点O运动，同时点Q从点C出发以2cm/s的速度沿射线CB运动，当点P到达终点O时，点Q也随之停止运动．设点P的运动时间为t（s）．（1）直接写出顶点D的坐标（______，______），对角线的交点E的坐标（______，______）；
（2）求对角线BD的长；
（3）是否存在t，使S△POQ=
SABCD，若存在，请求出的t值；不存在说明理由．（4）在整个运动过程中，PQ的中点到原点O的最短距离是______cm，（直接写出答案）
-
科目： 来源： 题型：
查看答案和解析>>【题目】立定跳远是体育中考选考项目之一，体育课上老师记录了某同学的一组立定跳远成绩如表：
成绩（m）
2.3
2.4
2.5
2.4
2.4
则下列关于这组数据的说法，正确的是（ ）
A.众数是2.3B.平均数是2.4
C.中位数是2.5D.方差是0.01
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，CE平分∠ACD，AE平分∠BAC，∠EAC+∠ACE=90°
（1）请判断AB与CD的位置关系并说明理由；
（2）如图2，当∠E=90°且AB与CD的位置关系保持不变，移动直角顶点E，使∠MCE=∠ECD，当直角顶点E点移动时，问∠BAE与∠MCD否存在确定的数量关系？并说明理由；
（3）如图3，P为线段AC上一定点，点Q为直线CD上一动点且AB与CD的位置关系保持不变，当点Q在射线CD上运动时（点C除外）∠CPQ+∠CQP与∠BAC有何数量关系？猜想结论并说明理由．
相关试题
