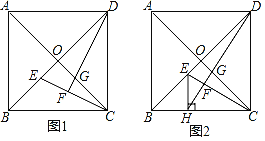
【题目】已知正方形ABCD的对角线AC,BD相交于点O.
(1)如图1,E,G分别是OB,OC上的点,CE与DG的延长线相交于点F.若DF⊥CE,求证:OE=OG;
(2)如图2,H是BC上的点,过点H作EH⊥BC,交线段OB于点E,连结DH交CE于点F,交OC于点G.若OE=OG,
①求证:∠ODG=∠OCE;
②当AB=1时,求HC的长.
参考答案:
【答案】(1)证明见解析;(2)①证明见解析;②![]()
【解析】试题分析:(1)欲证明OE=OG,只要证明△DOG≌△COE(ASA)即可;
(2)①欲证明∠ODG=∠OCE,只要证明△ODG≌△OCE即可;
②设CH=x,由△CHE∽△DCH,可得![]() ,即HC2=EHCD,由此构建方程即可解决问题;
,即HC2=EHCD,由此构建方程即可解决问题;
试题解析:(1)证明:如图1中,∵四边形ABCD是正方形,∴AC⊥BD,OD=OC,∴∠DOG=∠COE=90°,∴∠OEC+∠OCE=90°,∵DF⊥CE,∴∠OEC+∠ODG=90°,∴∠ODG=∠OCE,∴△DOG≌△COE(ASA),∴OE=OG.
(2)①证明:如图2中,∵OG=OE,∠DOG=∠COE=90°OD=OC,∴△ODG≌△OCE,∴∠ODG=∠OCE.
②解:设CH=x,∵四边形ABCD是正方形,AB=1,∴BH=1﹣x,∠DBC=∠BDC=∠ACB=45°,∵EH⊥BC,∴∠BEH=∠EBH=45°,∴EH=BH=1﹣x,∵∠ODG=∠OCE,∴∠BDC﹣∠ODG=∠ACB﹣∠OCE,∴∠HDC=∠ECH,∵EH⊥BC,∴∠EHC=∠HCD=90°,∴△CHE∽△DCH,∴![]() ,∴HC2=EHCD,∴x2=(1﹣x)1,解得x=
,∴HC2=EHCD,∴x2=(1﹣x)1,解得x=![]() 或
或![]() (舍弃),∴HC=
(舍弃),∴HC=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如下数表是由从1 开始的连续自然数组成,观察规律并完成各题的解答.

(1)表中第8行的最后一个数是_____,它是自然数_____的平方,第8行共有 _____个数;
(2)用含n的代数式表示:第n行的第一个数是_____,最后一个数是_____,第n行共有_____个数;
(3)求第n行各数之和.
-
科目: 来源: 题型:
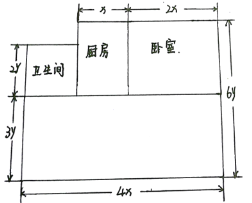
查看答案和解析>>【题目】如图是一套房子的平面图,尺寸如图.
(1)这套房子的总面积是多少?(用含x、y的代数式表示)
(2)如果x=1.8米,y=1米,那么房子的面积是多少平方米?如果每平方米房价为5万元,那么房屋总价多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于三角函数有如下公式:sin(α+β)=sinαcosβ+cosαsinβ,sin(α﹣β)=sinαcosβ﹣cosαsinβ
cos(α+β)=cosαcosβ﹣sinαsinβ,cos(α﹣β)=cosαcosβ+sinαsinβ
tan(α+β)=
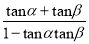 (1﹣tanαtanβ≠0)
(1﹣tanαtanβ≠0)tan(α﹣β)=
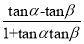 (1+tanαtanβ≠0)
(1+tanαtanβ≠0)利用这些公式可以将一些不是特殊角的三角函数转化为特殊角的三角函数来求值.
如:tan105°=tan(45°+60°)=

根据上面的知识,你可以选择适当的公式解决下面问题:
如图,两座建筑物AB和DC的水平距离BC为24米,从点A测得点D的俯角α=15°,测得点C的俯角β=75°,求建筑物CD的高度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】对于一元二次方程
 ,下列说法:①若a+c=0,方程
,下列说法:①若a+c=0,方程 有两个不等的实数根;②若方程
有两个不等的实数根;②若方程 有两个不等的实数根,则方程
有两个不等的实数根,则方程 也一定有两个不等的实数根;③若c是方程
也一定有两个不等的实数根;③若c是方程 的一个根,则一定有
的一个根,则一定有 成立;④若m是方程
成立;④若m是方程 的一个根,则一定有
的一个根,则一定有 成立.其中正确地只有 ( )
成立.其中正确地只有 ( )A. ①② B. ②③ C. ③④ D. ①④
-
科目: 来源: 题型:
查看答案和解析>>【题目】将下列各数填到相应的集合里:
-
 ,+5,-9,π,
,+5,-9,π, ,19, 1.2, 0,-5.26,0.8256…,5.3
,19, 1.2, 0,-5.26,0.8256…,5.3正数集合﹛ …﹜
负数集合﹛ …﹜
整数集合﹛ …﹜
分数集合﹛ …﹜
有理数集合﹛ …﹜
-
科目: 来源: 题型:
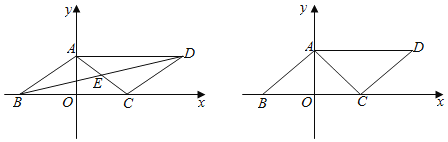
查看答案和解析>>【题目】如图,已知□ABCD边BC在x轴上,顶点A在y轴上,对角线AC所在的直线为y=
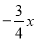 +6,且AC=AB,若点P从点A出发以1cm/s的速度向终点O运动,同时点Q从点C出发以2cm/s的速度沿射线CB运动,当点P到达终点O时,点Q也随之停止运动.设点P的运动时间为t(s).
+6,且AC=AB,若点P从点A出发以1cm/s的速度向终点O运动,同时点Q从点C出发以2cm/s的速度沿射线CB运动,当点P到达终点O时,点Q也随之停止运动.设点P的运动时间为t(s).(1)直接写出顶点D的坐标(______,______),对角线的交点E的坐标(______,______);
(2)求对角线BD的长;
(3)是否存在t,使S△POQ=
 SABCD,若存在,请求出的t值;不存在说明理由.
SABCD,若存在,请求出的t值;不存在说明理由.(4)在整个运动过程中,PQ的中点到原点O的最短距离是______cm,(直接写出答案)
相关试题

