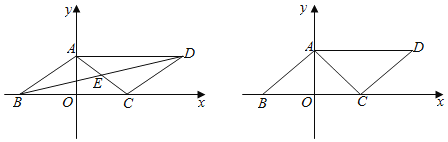
【题目】如图,已知□ABCD边BC在x轴上,顶点A在y轴上,对角线AC所在的直线为y=![]() +6,且AC=AB,若点P从点A出发以1cm/s的速度向终点O运动,同时点Q从点C出发以2cm/s的速度沿射线CB运动,当点P到达终点O时,点Q也随之停止运动.设点P的运动时间为t(s).
+6,且AC=AB,若点P从点A出发以1cm/s的速度向终点O运动,同时点Q从点C出发以2cm/s的速度沿射线CB运动,当点P到达终点O时,点Q也随之停止运动.设点P的运动时间为t(s).
(1)直接写出顶点D的坐标(______,______),对角线的交点E的坐标(______,______);
(2)求对角线BD的长;
(3)是否存在t,使S△POQ=![]() SABCD,若存在,请求出的t值;不存在说明理由.
SABCD,若存在,请求出的t值;不存在说明理由.
(4)在整个运动过程中,PQ的中点到原点O的最短距离是______cm,(直接写出答案)
参考答案:
【答案】(1)16;6;4;3;(2)BD=6![]() ;(3)存在,t值为2;(4)此时PQ的中点到原点O的最短距离为
;(3)存在,t值为2;(4)此时PQ的中点到原点O的最短距离为![]() .
.
【解析】
(1)令x=0,y=0代入解析式得出A,C坐标,进而利用平行四边形的性质解答即可;
(2)根据平行四边形的性质得出点B,D坐标,利用两点间距离解答即可;
(3)利用三角形的面积公式和平行四边形的面积公式列出方程解答即可;
(4)根据直角三角形斜边上中线等于斜边的一半可知,当PQ长度最短时,PQ的中点到原点O的距离最短解答即可.
(1)把x=0代入y=![]() +6,可得y=6,
+6,可得y=6,
即A的坐标为(0,6),
把y=0代入y=![]() +6,可得:x=8,
+6,可得:x=8,
即点C的坐标为(8,0),
根据平行四边形的性质可得:点B坐标为(-8,0),
所以AD=BC=16,
所以点D坐标为(16,6),
点E为对角线的交点,
故点E是AC的中点,
E的坐标为(4,3),
故答案为:16;6;4;3;
(2)因为B(-8,0)和D(16,6),
∴BD=![]() ;
;
(3)设时间为t,可得:OP=6-t,OQ=8-2t,
∵S△POQ= SABCD,
当0<t≤4时,![]() ,
,
解得:t1=2,t2=8(不合题意,舍去),
当4<t≤6时,![]() ,
,
△<0,不存在,
答:存在S△POQ=![]() SABCD,此时t值为2;
SABCD,此时t值为2;
(4)∵![]() ,
,
当t=![]() 时,PQ=
时,PQ=![]() ,
,
当PQ长度最短时,PQ的中点到原点O的距离最短,此时PQ的中点到原点O的最短距离为![]() PQ=
PQ=![]()
![]() =
=![]()
-
科目: 来源: 题型:
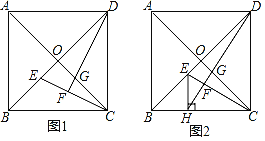
查看答案和解析>>【题目】已知正方形ABCD的对角线AC,BD相交于点O.
(1)如图1,E,G分别是OB,OC上的点,CE与DG的延长线相交于点F.若DF⊥CE,求证:OE=OG;
(2)如图2,H是BC上的点,过点H作EH⊥BC,交线段OB于点E,连结DH交CE于点F,交OC于点G.若OE=OG,
①求证:∠ODG=∠OCE;
②当AB=1时,求HC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于一元二次方程
 ,下列说法:①若a+c=0,方程
,下列说法:①若a+c=0,方程 有两个不等的实数根;②若方程
有两个不等的实数根;②若方程 有两个不等的实数根,则方程
有两个不等的实数根,则方程 也一定有两个不等的实数根;③若c是方程
也一定有两个不等的实数根;③若c是方程 的一个根,则一定有
的一个根,则一定有 成立;④若m是方程
成立;④若m是方程 的一个根,则一定有
的一个根,则一定有 成立.其中正确地只有 ( )
成立.其中正确地只有 ( )A. ①② B. ②③ C. ③④ D. ①④
-
科目: 来源: 题型:
查看答案和解析>>【题目】将下列各数填到相应的集合里:
-
 ,+5,-9,π,
,+5,-9,π, ,19, 1.2, 0,-5.26,0.8256…,5.3
,19, 1.2, 0,-5.26,0.8256…,5.3正数集合﹛ …﹜
负数集合﹛ …﹜
整数集合﹛ …﹜
分数集合﹛ …﹜
有理数集合﹛ …﹜
-
科目: 来源: 题型:
查看答案和解析>>【题目】立定跳远是体育中考选考项目之一,体育课上老师记录了某同学的一组立定跳远成绩如表:
成绩(m)
2.3
2.4
2.5
2.4
2.4
则下列关于这组数据的说法,正确的是( )
A.众数是2.3B.平均数是2.4
C.中位数是2.5D.方差是0.01
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,CE平分∠ACD,AE平分∠BAC,∠EAC+∠ACE=90°
(1)请判断AB与CD的位置关系并说明理由;
(2)如图2,当∠E=90°且AB与CD的位置关系保持不变,移动直角顶点E,使∠MCE=∠ECD,当直角顶点E点移动时,问∠BAE与∠MCD否存在确定的数量关系?并说明理由;
(3)如图3,P为线段AC上一定点,点Q为直线CD上一动点且AB与CD的位置关系保持不变,当点Q在射线CD上运动时(点C除外)∠CPQ+∠CQP与∠BAC有何数量关系?猜想结论并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)
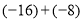
(2)
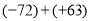
(3)0-(-5)
(4)-2.5-5.9
(5)12-(-18)+(-7)-15
(6)
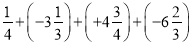
相关试题

