【题目】正方形网格中,小格的顶点叫做格点,以格点为顶点的三角形叫做格点三角形.下图![]() 中的正方形网格中
中的正方形网格中![]() 是格点三角形,小正方形网格的边长为
是格点三角形,小正方形网格的边长为![]() (单位长度).
(单位长度).
![]() 的面积是________(平方单位);
的面积是________(平方单位);
![]() 在图
在图![]() 所示的正方形网格中作出格点
所示的正方形网格中作出格点![]() 和
和![]() ″
″![]() ″
″![]() ″,使
″,使![]() ,
,![]() ″
″![]() ″
″![]() ″
″![]() ,且
,且![]() 、
、![]() 、
、![]() ″
″![]() ″中任意两条线段的长度都不相等;
″中任意两条线段的长度都不相等;
![]() 在所有与
在所有与![]() 相似的格点三角形中,是否存在面积为
相似的格点三角形中,是否存在面积为![]() (平方单位)的格点三角形?如果存在,请在图
(平方单位)的格点三角形?如果存在,请在图![]() 中作出,如果不存在,请说明理由.
中作出,如果不存在,请说明理由.

参考答案:
【答案】(1)5;(2)详见解析;(3)不存在.
【解析】
(1)△ABC的面积可以用正方形的面积减去其周围三个直角三角形的面积.
(2)利用格点正方形将三角形ABC的三边分别求出来,利用相似三角形对应边成比例得到相应的三角形的三边长,在格点正方形中画出来即可;
(3)假设存在这样的三角形,从存在出发,经过推理得到矛盾后即可说明不存在这样的三角形.
![]() ;
;
![]() 如图
如图
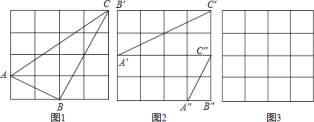
我们可以知道![]() 为
为![]() ,
,![]() 为
为![]() ,为
,为![]() 长的两倍.且
长的两倍.且![]() 与
与![]() 是垂直的.
是垂直的.
![]() 若存在该三角形,命名为
若存在该三角形,命名为![]() 与
与![]() 相似.
相似.
因为![]() 长为
长为![]() 长的两倍所以
长的两倍所以![]() 长为
长为![]() 长的两倍.
长的两倍.
![]() ,
,
![]() ,
,
而![]() 是不可能由格点三角形构成,所以不存在.
是不可能由格点三角形构成,所以不存在.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,AB=AC, ∠A=40°,O为边BC的中点,把△ABC绕O顺时针旋转m(0<m<180)度后,如果点B恰好落在初始△ABC的边上,那么m=_________
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,抛物线y=ax2+bx﹣2与x轴交于点A(﹣1,0),B(4,0)两点,与y轴交于点C,经过点B的直线交y轴于点E(0,2).
(1)求该抛物线的解析式;
(2)如图2,过点A作BE的平行线交抛物线于另一点D,点P是抛物线上位于线段AD下方的一个动点,连结PA,EA,ED,PD,求四边形EAPD面积的最大值;
(3)如图3,连结AC,将△AOC绕点O逆时针方向旋转,记旋转中的三角形为△A′OC′,在旋转过程中,直线OC′与直线BE交于点Q,若△BOQ为等腰三角形,请直接写出点Q的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=9,AC=6,BC=12,点M在AB边上,且AM=3,过点M作直线MN与AC边交于点N,使截得的三角形与原三角形相似,则MN=__.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在宽20米,长32米的矩形耕地上,修筑同样宽的三条路(两条纵向,一条横向,并且横向与纵向互相垂直),把这块耕地分成大小相等的六块试验田,要使试验田的面积是570平方米,问道路应该多宽?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将
 以直角顶点
以直角顶点 为旋转中心顺时针旋转,使点
为旋转中心顺时针旋转,使点 刚好落在
刚好落在 上(即:点
上(即:点 ),若
),若 ,则图中
,则图中


A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
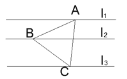
查看答案和解析>>【题目】如图所示,l1∥l2∥l3,l1、l2间的距离为3, l2、l3间的距离为6,等边△ABC三个顶点均在l1、l2、l3上,则△ABC的边长为________
相关试题

