【题目】抛物线y=mx2﹣2mx+m﹣3(m>0)在﹣1<x<0位于x轴下方,在3<x<4位于x轴上方,则m的值为 .
参考答案:
【答案】![]()
【解析】解:
∵抛物线y=mx2﹣2mx+m﹣3(m>0)的对称轴为直线x=1,
而在3<x<4位于x轴上方,
∴抛物线在﹣2<x<﹣1这一段位于x轴的上方,
∵在﹣1<x<0位于x轴下方,
∴抛物线过点(﹣1,0),
把(﹣1,0)代入y=mx2﹣2mx+m﹣3得m+2m+m﹣3=0,
解得m= ![]() ,
,
所以答案是: ![]() .
.
【考点精析】本题主要考查了抛物线与坐标轴的交点的相关知识点,需要掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为点D,若AD=BC,则sin∠A= .

-
科目: 来源: 题型:
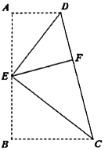
查看答案和解析>>【题目】如图,四边形
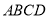 中,
中,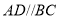 ,
,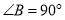 ,
, 为
为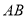 上一点,分别以
上一点,分别以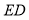 ,
,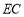 为折痕将两个角(
为折痕将两个角(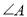 ,
,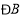 )向内折起,点
)向内折起,点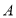 ,
,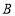 恰好都落在
恰好都落在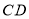 边的点
边的点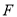 处.若
处.若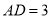 ,
,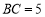 ,则
,则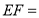 ________.
________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有个填写运算符号的游戏:在“ 1□3□9□7” 中的每个□内,填入
 ,
, ,
, ,
, 中的某一个(可重复使用),然后计算结果.
中的某一个(可重复使用),然后计算结果.(1)计算:
 ;
;(2)若1
 3×9□7= -4,请推算□内的符号;
3×9□7= -4,请推算□内的符号;(3)在“1□3□9-7”的□内填入符号后,使计算所得数最小,直接写出这个最小数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
 中,
中, ,
, ,
, .
.
(1)求证:
 ;
;(2)若
 ,
, ,
, ,
, 分别是
分别是 ,
, ,
, ,
, 的中点,求证:线段
的中点,求证:线段 与线段
与线段 互相平分.
互相平分. -
科目: 来源: 题型:
查看答案和解析>>【题目】探究:如图,在正方形
 中,点
中,点 ,
, 分别为边
分别为边 ,
, 上的动点,且
上的动点,且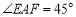 .
.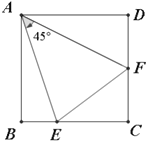
(1)如果将
 绕点
绕点 顺时针方向旋转
顺时针方向旋转 .请你画出图形(旋转后的辅助线).你能够得出关于
.请你画出图形(旋转后的辅助线).你能够得出关于 ,
, ,
, 的一个结论是________.
的一个结论是________.(2)如果点
 ,
, 分别运动到
分别运动到 ,
, 的延长线上,如图,请你能够得出关于
的延长线上,如图,请你能够得出关于 ,
, ,
, 的一个结论是________.
的一个结论是________.
(3)变式:如图,将题目改为“在四边形
 中,
中, ,且
,且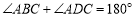 ,点
,点 ,
, 分别为边
分别为边 ,
, 上的动点,且
上的动点,且 ”,请你猜想关于
”,请你猜想关于 ,
, ,
, 有什么关系?并验证你的猜想.
有什么关系?并验证你的猜想.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC 中,点 D 是边 BC 上的点(与 B、C 两点不重合),过点 D作 DE∥AC,DF∥AB,分别交 AB、AC 于 E、F 两点,下列说法正确的是( )

A. 若 AD 平分∠BAC,则四边形 AEDF 是菱形
B. 若 BD=CD,则四边形 AEDF 是菱形
C. 若 AD 垂直平分 BC,则四边形 AEDF 是矩形
D. 若 AD⊥BC,则四边形 AEDF 是矩形
相关试题

