【题目】已知λ∈R,函数f(x)=ex﹣ex﹣λ(xlnx﹣x+1)的导数为g(x).
(1)求曲线y=f(x)在x=1处的切线方程;
(2)若函数g(x)存在极值,求λ的取值范围;
(3)若x≥1时,f(x)≥0恒成立,求λ的最大值.
参考答案:
【答案】
(1)解:)f(x)=ex﹣ex﹣λ(xlnx﹣x+1)的定义域为(0,+∞).
f′(x)=ex﹣e﹣λlnx,f′(1)=0,又f(1)=0.
曲线y=f(x)在x=1处的切线方程为y=0
(2)解:∵g(x)=f′(x)=ex﹣e﹣λlnx,(x>0),g′(x)= ![]()
函数g(x)存在极值,即方程 ![]() 有正实数根,
有正实数根,
λ=xex,(x>0),
令G(x)=xex,G′(x)=x(ex+1)>0在(0,+∞)恒成立.
x∈(0,+∞)时,G(x)>0,
∴函数g(x)存在极值,λ的取值范围为(0,+∞)
(3)解:由(1)、(2)可知f(1)=0,f′(1)=g(1)=0
结合(2)x≥1时,g′(x)= ![]() ≥0,可得λ≤xex,(x≥1),
≥0,可得λ≤xex,(x≥1),
G(x)=xex,在(1,+∞)恒成立.
∴λ≤e时,g′(x)≥0,g(x)在[1,+∞)递增,g(x)≥g(1)=0
故f(x)在[1,+∞)递增,∴f(x)≥f(1)=0.
当λ>e时,存在x0>1,使g′(x)=0,∴x∈(1,x0)时,g′(x)<0,
即x∈(1,x0)时,g(x)递减,而g(1)=0,
∴x∈(1,x0)时,g(x)<0,此时f(x)递减,而f(1)=0,
∴在(1,x0),f(x)<0,故当λ>e时,f(x)≥0不恒成立;
综上x≥1时,f(x)≥0恒成立,λ的最大值为e
【解析】(1)求出f′(x)=ex﹣e﹣λlnx,f′(1)=0,又f(1)=0,得到曲线y=f(x)在x=1处的切线方程为y=0.(2)g(x)=f′(x)=ex﹣e﹣λlnx(x>0),g′(x)= ![]() ,函数g(x)存在极值,即方程
,函数g(x)存在极值,即方程 ![]() 有正实数根,λ=xex , (x>0),可得λ的取值范围.(3)由(1)、(2)可知f(1)=0,f′(1)=g(1)=0,结合(2)分λ≤e,λ>e,讨论x≥1时,是否f(x)≥0恒成立,即可.
有正实数根,λ=xex , (x>0),可得λ的取值范围.(3)由(1)、(2)可知f(1)=0,f′(1)=g(1)=0,结合(2)分λ≤e,λ>e,讨论x≥1时,是否f(x)≥0恒成立,即可.
【考点精析】本题主要考查了函数的极值与导数和函数的最大(小)值与导数的相关知识点,需要掌握求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值;求函数
是极小值;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.
比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在水域上建一个演艺广场,演艺广场由看台Ⅰ,看台Ⅱ,三角形水域ABC,及矩形表演台BCDE四个部分构成(如图),看台Ⅰ,看台Ⅱ是分别以AB,AC为直径的两个半圆形区域,且看台Ⅰ的面积是看台Ⅱ的面积的3倍,矩形表演台BCDE 中,CD=10米,三角形水域ABC的面积为
 平方米,设∠BAC=θ.
平方米,设∠BAC=θ. 
(1)求BC的长(用含θ的式子表示);
(2)若表演台每平方米的造价为0.3万元,求表演台的最低造价. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xoy中,椭圆
 的右顶点和上顶点分别为点A,B,M是线段AB的中点,且
的右顶点和上顶点分别为点A,B,M是线段AB的中点,且 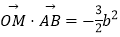 ..
.. 
(1)求椭圆的离心率;
(2)若a=2,四边形ABCD内接于椭圆,AB∥CD,记直线AD,BC的斜率分别为k1 , k2 , 求证:k1k2为定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知常数p>0,数列{an}满足an+1=|p﹣an|+2an+p,n∈N*.
(1)若a1=﹣1,p=1, ①求a4的值;
②求数列{an}的前n项和Sn;
(2)若数列{an}中存在三项ar , as , at(r,s,t∈N*,r<s<t)依次成等差数列,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是⊙O的内接四边形,若∠BOD=88°,则∠BCD的度数是( )
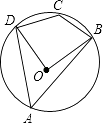
A.88°
B.92°
C.106°
D.136° -
科目: 来源: 题型:
查看答案和解析>>【题目】反比例函数y=
 的图象如图所示,以下结论: ①常数m<﹣1;
的图象如图所示,以下结论: ①常数m<﹣1;
②在每个象限内,y随x的增大而增大;
③若A(﹣1,h),B(2,k)在图象上,则h<k;
④若P(x,y)在图象上,则P′(﹣x,﹣y)也在图象上.
其中正确的是( )
A.①②
B.②③
C.③④
D.①④ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,函数y=ax2+bx+c(a≠0)的图象与x轴相交于A、B两点,頂点为点M.則下列说法不正确的是( )
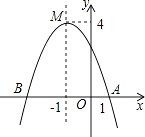
A.a<0
B.当x=﹣1时,函数y有最小值4
C.对称轴是直线=﹣1
D.点B的坐标为(﹣3,0)
相关试题

