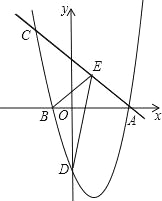
【题目】如图，抛物线y=+bx﹣4（a≠0）与x轴交于A（4，0），B（﹣1，0）两点，过点A的直线y=﹣x+4交抛物线于点C．

（1）求此抛物线的解析式；

（2）在直线AC上有一动点E，当点E在某个位置时，使△BDE的周长最小，求此时E点坐标．

参考答案：

【答案】(1) y=﹣3x﹣4；(2) E（，）．

【解析】

试题分析：（1）直接把点A（4，0），B（﹣1，0）代入抛物线y=+bx﹣4求出a、b的值，进而可得出抛物线的解析式；

（2）先判断出周长最小时BE⊥AC，即作点B关于直线AC的对称点F，连接DF，交AC于点E，联立方程组即可．

试题解析：（1）∵抛物线y=+bx﹣4与x轴交于两点A（4，0），B（﹣1，0），

∴，解得，

∴此抛物线的解析式为：y=﹣3x﹣4；

（2）如图1，作点B关于直线AC的对称点F，连接DF交AC于点E，

由（1）得，抛物线解析式为y=﹣3x﹣4，

∴D（0，﹣4），

∵直线y=﹣x+4交抛物线于点C，

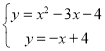∴，解得，或，

∴C（﹣2，6），

∵A（4，0），

∵直线AC解析式为y=﹣x+4，直线BF⊥AC，且B（﹣1，0），

∴直线BF解析式为y=x+1，

设点F（m，m+1），

∴G（，），

∵点G在直线AC上，

∴+4=，

∴m=4，

∴F（4，5），

∵D（0，﹣4），

∴直线DF解析式为y=x﹣4，

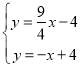解得，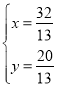

∴直线DF和直线AC的交点E（，）．

关闭