【题目】如图,四边形ABCD中,AB=AD=2,∠A=60°,BC=![]() ,CD=3.
,CD=3.
(1)求∠ADC的度数;
(2)求四边形ABCD的面积.

参考答案:
【答案】(1)150°; (2)![]()
【解析】试题分析:
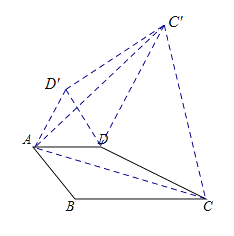
(1)将△ABC绕点逆时针旋转60°,则有等边△ACC′,点D到等边△ACC′的距离符合勾股定理的逆定理,故将△ADC绕点A逆时针旋转60°,即可求解.
(2)将四边形ABCD分割为等边三角形和直角三角形,分别求出等边三角形和直角三角形的面积即可.
试题解析:
(1)如图,把△ABC绕点A逆时针旋转60°,构成三角形ACC′,把△ADC绕点A逆时针旋转60°,构成△AD′C.
由旋转的性质可知,△ACC′与△ADD′是等边三角形,且DC′=BC=![]() ,AD′=DD′=AD=2,D′C′=DC=3,∠AD′C=∠ADC.
,AD′=DD′=AD=2,D′C′=DC=3,∠AD′C=∠ADC.
因为DD′2=4,D′C′2=9,DC′2=13,所以DD′2+D′C′2=DC′2.
所以△DD′C′是直角三角形,所以∠DD′C′=90°,
因为∠AD′D=60°,所以∠AD′C=60°+90°=150°.
所以∠ADC=150°.
(2)由(1)知,S四边形ABCD=S四边形ADC′D′.
S四边形ADC′D′=S等边△ADD′+SRt△DD′C′=![]() =3+
=3+![]() .
.
-
科目: 来源: 题型:
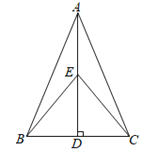
查看答案和解析>>【题目】如图,在等腰△ABC中,AD是底边BC边上的高,点E是AD上的一点.
(1)求证:△BEC是等腰三角形.
(2)若AB=AC=13,BC=10,点E是AD的中点,求BE的长.
-
科目: 来源: 题型:
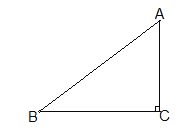
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,AB=5cm,BC=4cm,若点P从点A出发,以每秒2cm的速度沿折线A﹣B﹣C﹣A运动,设运动时间为t秒(t>0).
(1)若点P在BC上,且满足PA=PB,求此时t的值;
(2)若点P恰好在∠ABC的角平分线上,求此时t的值;
(3)在运动过程中,当t为何值时,△ACP为等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简下列各题
(1)-2a2b-3ab2+3a2b-4ab2;
(2)2(xyz-3x)+5(2x-3xyz);
-
科目: 来源: 题型:
查看答案和解析>>【题目】绝对值大于1且小于3的整数有______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为进一步发展基础教育,自2014年以来,某县加大了教育经费的投入,2014年该县投入教育经费6000万元.2016年投入教育经费8640万元.假设该县这两年投入教育经费的年平均增长率相同.
(1)求这两年该县投入教育经费的年平均增长率;
(2)若该县教育经费的投入还将保持相同的年平均增长率,请你预算2017年该县投入教育经费多少万元.
-
科目: 来源: 题型:
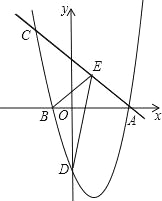
查看答案和解析>>【题目】如图,抛物线y=
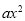 +bx﹣4(a≠0)与x轴交于A(4,0),B(﹣1,0)两点,过点A的直线y=﹣x+4交抛物线于点C.
+bx﹣4(a≠0)与x轴交于A(4,0),B(﹣1,0)两点,过点A的直线y=﹣x+4交抛物线于点C.(1)求此抛物线的解析式;
(2)在直线AC上有一动点E,当点E在某个位置时,使△BDE的周长最小,求此时E点坐标.
相关试题

