【题目】星光橱具店购进电饭煲和电压锅两种电器进行销售,其进价与售价如表:
进价(元/个) | 售价(元/个) | |
电饭煲 | 200 | 250 |
电压锅 | 160 | 200 |
(1)一季度,橱具店购进这两种电器共30台,用去了5600元,并且全部售完,问橱具店在该买卖中赚了多少钱?
(2)为了满足市场需求,二季度橱具店决定用不超过9000元的资金采购电饭煲和电压锅共50个,且电饭煲的数量不少于23个,问橱具店有哪几种进货方案?并说明理由;
(3)在(2)的条件下,请你通过计算判断,哪种进货方案橱具店赚钱最多?
参考答案:
【答案】(1)橱具店在该买卖中赚了1400元; (2)有三种方案,具体方案及理由见解析;(3)购进电饭煲,电压锅各25台时利润最大.
【解析】试题分析:(1)设橱具店购进电饭煲x台,电压锅y台,根据图表中的数据列出关于x、y的方程组并解方程组即可,等量关系是:这两种电器共30台、共用去5600元;
(2)设购买电饭煲a台,则购买电压锅(50﹣a)台,根据“二季度橱具店决定用不超过9000元的资金采购电饭煲和电压锅共50个,且电饭煲的数量不少于23个”列出不等关系即可解答;
(3)结合(2)中的数据进行计算即可.
试题解析:(1)设橱具店购进电饭煲x台,电压锅y台,依题意得![]() ,解得
,解得![]() ,所以,20×50+10×40=1400(元).
,所以,20×50+10×40=1400(元).
答:橱具店在该买卖中赚了1400元.
(2)设购买电饭煲a台,则购买电压锅(50﹣a)台,依题意得
200a+160(50-a)≤9000,
解得a≤25.
∵a≥23,∴23≤ a≤25.
又∵a为正整数,∴a可取23,24,25.
故有三种方案:①购买电饭煲23台,则购买电压锅27台;
②购买电饭煲24台,则购买电压锅26台;
③购买电饭煲25台,则购买电压锅25台.
(3)设橱具店赚钱数额为W元,
当a=23时,W=23×50+27×40=2230;
当a=24时,W=24×50+26×40=2240;
当a=25时,W=25×50+25×40=2250.
综上所述,当a=25时,W最大,
此时购进电饭煲,电压锅各25台.
-
科目: 来源: 题型:
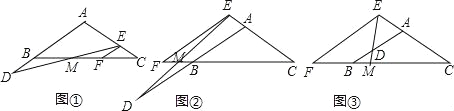
查看答案和解析>>【题目】在等腰三角形ABCD中,AB=AC,分别在射线AB、CA上取点D、E,连结DE,过点E作EF∥AB交直线BC于点F,直线BC与DE所在直线交于点M.
猜想:如图①,点D在边AB延长线上,点E在边AC上,且BD=CE,则线段BM、EM的大小关系为 .
探究:如图②,点D、E分别在边AB、CA延长线上,且BD=CE,判断线段DM、EM的大小关系,并加以证明.
拓展:如图③,点D在边AB上(点D不与点A、B重合),点E在边CA的延长线上,其它条件不变,若BD=1,CE=4,DM=0.7,则线段DE的长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程x2+2x+1=4较适宜的方法是( )
A. 实验法 B. 公式法 C. 因式分解法 D. 配方法
-
科目: 来源: 题型:
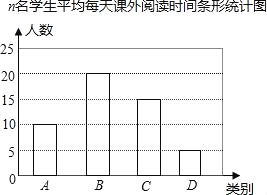
查看答案和解析>>【题目】课外阅读是提高学生素养的重要途径,某校团委为了解学生课外阅读情况,随机抽查了本校n名学生,统计它们平均每天课外阅读时间t(时),并根据时间t的长短分为A、B、C、D四类,(A)0<t<0.5,(B)0.5≤t<1,(C)1≤t<1.5,(D)t≥1.5,并根据抽查的人数绘制如下统计图.
(1)求n的值.
(2)四类中人数最多的是 (用A、B、C、D作答),选择该类的学生人数占被调查的学生人数的百分比为 .
(3)该校现有1300名学生,估计该校学生课外阅读时间不少于1小时的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】命题“相等的角是对顶角”的逆命题是_____________________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把方程3x(x﹣2)=4(x+1)化为一元二次方程的一般形式是_______;
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形的周长为30,腰长是12,则底边长为.
相关试题

