【题目】如图,在△ABC中,AB=AC,∠ABC=72°.

(1)用直尺和圆规作∠ABC的平分线BD交AC于点D(保留作图痕迹,不要求写作法);
(2)在(1)中作出∠ABC的平分线BD后,求∠BDC的度数.
参考答案:
【答案】(1)作图如下:(2)∠BDC=72°
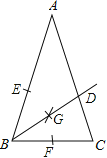
【解析】解:(1)作图如下:

(2)∵在△ABC中,AB=AC,∠ABC=72°,
∴∠A=180°﹣2∠ABC=180°﹣144°=36°。
∵AD是∠ABC的平分线,∴∠ABD=![]() ∠ABC=
∠ABC=![]() ×72°=36°。
×72°=36°。
∵∠BDC是△ABD的外角,∴∠BDC=∠A+∠ABD=36°+36°=72°。
(1)根据角平分线的作法利用直尺和圆规作出∠ABC的平分线:
①以点B为圆心,任意长为半径画弧,分别交AB、BC于点E、F;
②分别以点E、F为圆心,大于![]() EF为半径画圆,两圆相较于点G,连接BG交AC于点D。
EF为半径画圆,两圆相较于点G,连接BG交AC于点D。
(2)先根据等腰三角形的性质及三角形内角和定理求出∠A的度数,再由角平分线的性质得出
∠ABD的度数,再根据三角形外角的性质得出∠BDC的度数即可。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=8,AD=6,将矩形ABCD绕点B按顺时针方向旋转后得到矩形A′BC′D′.若边A′B交线段CD于H,且BH=DH,则DH的值是( )

A.
B.
C.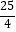
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】李克强总理连续三年把“全民阅读”写入《政府工作报告》,足以说明阅读的重要性.某校为了解学生最喜爱的书籍的类型,随机抽取了部分学生进行调查,并绘制了如下的条形统计图(部分信息未给出).已知,这些学生中有15%的人喜欢漫画,喜欢小说名著的人数是喜欢童话的
 ,请完成下列问题:
,请完成下列问题:
(1)求本次抽取的学生人数;
(2)喜欢小说名著、喜欢童话故事的学生各有多少人?并补全条形统计图;
(3)全校共有2100名学生,请估计最喜欢“小说名著”的人数有多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O中,点A为
 中点,BD为直径,过A作AP∥BC交DB的延长线于点P.
中点,BD为直径,过A作AP∥BC交DB的延长线于点P.
(1)求证:PA是⊙O的切线;
(2)若 ,AB=6,求sin∠ABD的值.
,AB=6,求sin∠ABD的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】张师傅驾车从甲地去乙地,途中在加油站加了一次油,加油时,车载电脑显示还能行驶50千米.假设加油前、后汽车都以100千米/小时的速度匀速行驶,已知油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示.

(1)求张师傅加油前油箱剩余油量y(升)与行驶时间t(小时)之间的关系式;
(2)求出a的值;
(3)求张师傅途中加油多少升? -
科目: 来源: 题型:
查看答案和解析>>【题目】为创建“绿色学校”,绿化校园环境,我校计划分两次购进A、B两种花草,第一次分别购进A、B两种花草30棵和15棵,共花费675元;第二次分别购进A、B两种花草12棵和5棵,共花费265元(两次购进同种花草价格相同).
(1)A、B两种花草每棵的价格分别是多少元?
(2)若购买A、B两种花草共30棵,且B种花草的数量不高于A种花草的数量的2倍,请你给出一种费用最省的方案,并求出该方案所需费用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:有一个内角为90°,且对角线相等的四边形称为准矩形.

(1)①如图1,准矩形ABCD中,∠ABC=90°,若AB=2,BC=3,则BD=;
②如图2,直角坐标系中,A(0,3),B(5,0),若整点P使得四边形AOBP是准矩形,则点P的坐标是;(整点指横坐标、纵坐标都为整数的点)
(2)如图3,正方形ABCD中,点E、F分别是边AD、AB上的点,且CF⊥BE,求证:四边形BCEF是准矩形;
(3)已知,准矩形ABCD中,∠ABC=90°,∠BAC=60°,AB=2,当△ADC为等腰三角形时,请直接写出这个准矩形的面积是 .
相关试题

