【题目】在一节数学课上,刘老师请同学们心里想一个非零的有理数,然后把这个数按照下面的程序进行计算后,刘老师立刻说出计算结果.

(1)若小明同学心里想的数是8,请列出算式并计算最后的结果;
(2)小明又试了几个数进行计算,发现结果都相等,于是小明把心里想的这个数记作a(a≠0),并按照程序通过计算进行验证,请你写出这个验证过程.
参考答案:
【答案】(1)列式:[(8+2)2-(8-2)2]×(-25)÷8;-200;(2)-200
【解析】
(1)先列式,再根据有理数混合运算法则计算即可得到结果;
(2)设这个数为a,根据题意列出代数式,去括号整理即可得到结果.
(1)列式:[(8+2)2-(8-2)2]×(-25)÷8.
原式=(100-36)×(-25)÷8=64×(-25)÷8=-200.
(2)根据题意,得:[(a+2)2-(a-2)2]×(-25)÷a=8a×(-25)÷a=-200.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀平均分成4 个小长方形,然后按图2的形状拼成一个正方形.
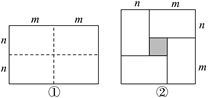
(1)图2中阴影部分的面积为 ;
(2)观察图2,请你写出式子(m+n)2,(m-n)2,mn之间的等量关系: ;
(3)若x+y=-6,xy=2.75,求x-y的值
-
科目: 来源: 题型:
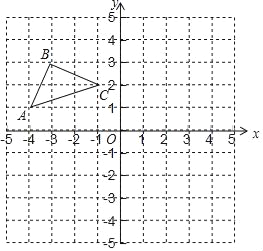
查看答案和解析>>【题目】如图,在平面直角坐标系中,点O为坐标原点,已知△ABC三个定点坐标分别为A(﹣4,1),B(﹣3,3),C(﹣1,2).
(1)画出△ABC关于x轴对称的△A1B1C1,点A,B,C的对称点分别是点A1、B1、C1,直接写出点A1,B1,C1的坐标;
(2)画出点C关于y轴的对称点C2,连接C1C2,CC2,C1C,求△CC1C2的面积.
-
科目: 来源: 题型:
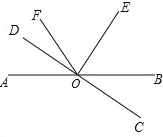
查看答案和解析>>【题目】如图,直线AB与CD相交于点0,∠AOD=20°,∠DOF:∠FOB=1:7,射线OE平分∠BOF.
(1)求∠EOB的度数;
(2)射线OE与直线CD有什么位置关系?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道:任意一个有理数与无理数的和为无理数,任意一个不为零的有理数与一个无理数的积为无理数,而零与无理数的积为零.由此可得:如果ax+b=0,其中a、b为有理数,x为无理数,那么a=0且b=0.
运用上述知识,解决下列问题:
(1)如果(a-2)
 +b+3=0,其中a、b为有理数,那么a= ,b= ;
+b+3=0,其中a、b为有理数,那么a= ,b= ;(2)如果(2+
 )a-(1-
)a-(1- )b=5,其中a、b为有理数,求a+2b的值.
)b=5,其中a、b为有理数,求a+2b的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2+bx+c与x轴分别交于A(﹣1,0),B(5,0)两点.
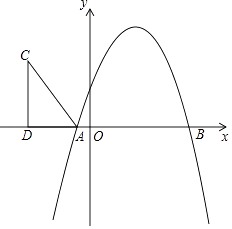
(1)求抛物线的解析式;
(2)在第二象限内取一点C,作CD垂直X轴于点D,链接AC,且AD=5,CD=8,将Rt△ACD沿x轴向右平移m个单位,当点C落在抛物线上时,求m的值;
(3)在(2)的条件下,当点C第一次落在抛物线上记为点E,点P是抛物线对称轴上一点.试探究:在抛物线上是否存在点Q,使以点B、E、P、Q为顶点的四边形是平行四边形?若存在,请出点Q的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算机系统对文件的管理通常采用树形目录结构,方式如图,在一个根目录下建立若干子目录(这里称第一层目录),每个子目录又可作为父目录,向下继续建立其子目录(这里称第二层目录),依次进行,可创建多层目录.现在一根目录下建立了四层目录,并且每一个父目录下的子目录的个数都相同,都等于根目录下目录的个数.已知第三层目录共有343个,求这一根目录下的所有目录的个数.

相关试题

