【题目】△![]() 中,
中, ![]() .取
.取![]() 边的中点
边的中点![]() ,作
,作![]() ⊥
⊥![]() 于点
于点![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() ,
, ![]() 交于点
交于点![]() .
.
(1)如图1,如果![]() ,求证:
,求证: ![]() ⊥
⊥![]() 并求
并求![]() 的值;
的值;
(2)如图2,如果![]() ,求证:
,求证: ![]() ⊥
⊥![]() 并用含
并用含![]() 的式子表示
的式子表示![]() .
.

参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:连接AD,根据等腰三角形的性质可得∠ABC=∠C,∠BAD=![]() ∠BAC,AD⊥BC,然后根据同角的余角相等可得∠ADE=∠C.易证△ADB∽△DEC,可得ADCE=BDDE.由此可得ADCE=
∠BAC,AD⊥BC,然后根据同角的余角相等可得∠ADE=∠C.易证△ADB∽△DEC,可得ADCE=BDDE.由此可得ADCE=![]() BC2DF=BCDF,即
BC2DF=BCDF,即![]() ,由此可证到△AFD∽△BEC,则有
,由此可证到△AFD∽△BEC,则有![]() ,在Rt△ADB中根据三角函数的定义可得tan∠ABD=tan(90°-
,在Rt△ADB中根据三角函数的定义可得tan∠ABD=tan(90°-![]() ∠BAC)=
∠BAC)=![]() ,从而可得
,从而可得![]() =
=![]() tan(90°-
tan(90°-![]() ∠BAC).由△AFD∽△BEC可得∠DAF=∠CBE,即可得到∠DAF+∠AOH=∠CBE+∠BOD=90°,即可得到∠AHB=90°.利用以上结论即可解决题中的两个问题.
∠BAC).由△AFD∽△BEC可得∠DAF=∠CBE,即可得到∠DAF+∠AOH=∠CBE+∠BOD=90°,即可得到∠AHB=90°.利用以上结论即可解决题中的两个问题.
试题解析:如图1,连接AD,
∵AB=AC,点D是BC的中点,
∴∠ABC=∠C,∠BAD=∠DAC=![]() ∠BAC,AD⊥BC,
∠BAC,AD⊥BC,
∵AD⊥BC,DE⊥AC,
∴∠ADE+∠CDE=90°,∠C+∠CDE=90°,
∴∠ADE=∠C.
又∵∠ADB=∠DEC=90°,
∴△ADB∽△DEC,
∴![]() ,
,
即ADCE=BDDE.
∵点D是BC的中点,点F是DE的中点,
∴BD=![]() BC,DE=2DF,
BC,DE=2DF,
∴ADCE═![]() BC2DF=BCDF,
BC2DF=BCDF,
∴![]() ,
,
又∵∠ADE=∠C,
∴△AFD∽△BEC,
∴![]() ,
,
在Rt△ADB中,
∵∠ABD=90°-∠BAD=90°-![]() ∠BAC,BD=
∠BAC,BD=![]() BC,
BC,
∴tan∠ABD=tan(90°-![]() ∠BAC)=
∠BAC)=![]() ,
,
∴![]() =
=![]() tan(90°-
tan(90°-![]() ∠BAC).
∠BAC).
∵△AFD∽△BEC,
∴∠DAF=∠CBE.
∵∠CBE+∠BOD=90°,∠AOH=∠BOD,
∴∠DAF+∠AOH=∠CBE+∠BOD=90°,
∴∠AHO=180°-90°=90°,即∠AHB=90°,
(1)如图1,
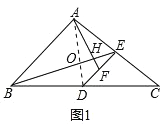
根据以上结论可得:
∠AHB=90°,![]() =
=![]() tan(90°-
tan(90°-![]() ×90°)=
×90°)=![]() ;
;
∴AF⊥BE, ![]() =
=![]() ;
;
(2)如图2,
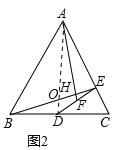
根据以上结论可得:∠AHB=90°,![]() =
=![]() tan(90°-
tan(90°-![]() α);
α);
∴AF⊥BE, ![]() =
=![]() tan(90°-
tan(90°-![]() α).
α).
-
科目: 来源: 题型:
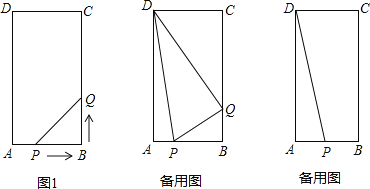
查看答案和解析>>【题目】在矩形ABCD中,AB=6cm,BC=12cm,点P从点A出发,沿AB边向点B以每秒1cm的速度移动,同时,点Q从点B出发沿BC边向点C以每秒2cm的速度移动.如果P、Q两点在分别到达B、C两点后就停止移动,回答下列问题:
(1)运动开始后第几秒时,△PBQ的面积等于8cm2?
(2)当运动开始后
 秒时,试判断△DPQ的形状;
秒时,试判断△DPQ的形状;(3)在运动过程中,是否存在这样的时刻,使以Q为圆心,PQ为半径的圆正好经过点D?若存在,求出运动时间;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某青年旅社有60间客房供游客居住,在旅游旺季,当客房的定价为每天200元时,所有客房都可以住满.客房定价每提高10元,就会有1个客房空闲,对有游客入住的客房,旅社还需要对每个房间支出20元/每天的维护费用,设每间客房的定价提高了x元.
(1)填表(不需化简)
入住的房间数量
房间价格
总维护费用
提价前
60
200
60×20
提价后
(2)若该青年旅社希望每天纯收入为14000元且能吸引更多的游客,则每间客房的定价应为多少元?(纯收入=总收入﹣维护费用)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC和△DCB中,AB=DC,AC=DB,AC与DB交于点M.
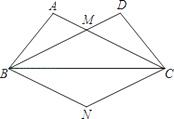
(1)求证:△ABC≌△DCB;
(2)过点C作CN∥BD,过点B作BN∥AC,CN与BN交于点N,试判断线段BN与CN的数量关系,并证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了更好的开展“学校特色体育教育”,从全校八年级各班随机抽取了60学生,进行各项体育项目的测试,了解他们的身体素质情况.下表是整理样本数据,得到的关于每个个体的测试成绩的部分统计表、图:

(说明:40—55分为不合格,55—70分为合格,70—85分为良好,85—100分为优秀)
请根据以上信息,解答下列问题:
(1)表中的
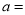 ;
; 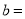 ;
; 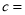 ;
;  .
.(2)请根据频数分布表,画出相应的频数分布直方图.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数
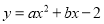 的图像交
的图像交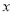 轴于
轴于 ,交
,交 轴于点
轴于点 ,连接直线
,连接直线 .
.(1)求二次函数的解析式;
(2)点
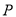 在二次函数的图像上,圆
在二次函数的图像上,圆 与直线
与直线 相切,切点为
相切,切点为 .
.①若
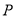 在
在 轴的左侧,且△
轴的左侧,且△ ∽△
∽△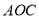 ,求点
,求点 的坐标;
的坐标;②若圆
 的半径为4,求点
的半径为4,求点 的坐标.
的坐标.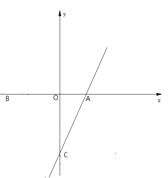
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中:①有公共顶点且相等的角是对顶角;②直线外一点到这条直线的垂线段,叫做点到直线的距离;③互为邻补角的两个角的平分线互相垂直;④经过一点有且只有一条直线与已知直线平行.其中真命题的个数有( )
A.1个B.2个C.3个D.4个
相关试题

