【题目】如图一:在Rt△ABC中,∠C=90°AD、BE分别是△ABC中∠A、∠B的平分线,AD、BE交于点F,过F点做FH⊥AD交AC于点H,易证:AH+DB=AB;
(1)若将Rt△ABC中∠BAC、∠ABC的内角平分线改成外角平分线,即:AF、BF分别是∠BAC、∠ABC的外角平分线交于F点,FH⊥AF交直线AC于H点,如图二:请写出线段AH、BD、AB之间的数量关系,并证明。
(2)若将Rt△ABC中∠BAC、∠ABC的内角平分线改成一个是外角平分线,即:AF是∠A的内角平分线,BE是∠B的外角平分线交于F点,FH⊥AD交AC于点H.如图三:请写出线段AH、BD、AB之间的数量关系,无需证明。

参考答案:
【答案】(1) AH=AB+BD ,证明见解析;(2) AH=AB+BD
【解析】(1)的结论是:AH=AB+BD
(2)的结论是:AH=AB+BD
(1)的结论证明如下:
∵AF平分∠BAH
∴∠BAF=∠HAF
∵AF⊥HM
∴△HAF≌△MAF
∴AH=AM ∠AHF=∠M
∵AF平分∠BAH
∴∠ABF=∠FBN
∵∠AHF+∠HAF=90°
∵∠DAC+∠ADB=90°
∴∠ADB=∠AHF
∴∠FDB=∠BMF
∴△DFB≌△MFB
∴DB=BM
∵AM=AB+BM
∴AH=AB+DB
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线AB平移至△FEG,DE、FG相交于点H.

(1)判断线段DE、FG的位置关系,并说明理由;
(2)连结CG,求证:四边形CBEG是正方形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,CD的中点,连接BM,MN,BN.

(1)求证:BM=MN;
(2)∠BAD=60°,AC平分∠BAD,AC=2,求BN的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】若一元二次方程x2+2x+m+1=0有实数根,则( )
A.m的最小值是1
B.m的最小值是﹣1
C.m的最大值是0
D.m的最大值是2 -
科目: 来源: 题型:
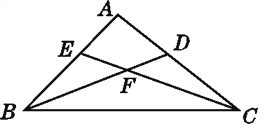
查看答案和解析>>【题目】如图,以CD为公共边的三角形是____________;∠EFB是____________的内角;在△BCE中,BE所对的角是____________,∠CBE所对的边是____________;以∠A为公共角的三角形是____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.a3a2=a6B.(ab3)2=a2b6
C.(a﹣b)2=a2﹣b2D.5a﹣3a=2
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:抛物线y=x2+4x+4+m的图像与y轴交于点C,点B与点C的纵坐标相同,一次函数y=kx+b的与二次函数交于A、B两点,且A点坐标为(-1,0).
(1)求二次函数与一次函数的解析式;
(2)若抛物线对称轴上存在一点P,直线PC将△ABC分成面积为1:2两部分,求P点坐标。

相关试题

