【题目】如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,CD的中点,连接BM,MN,BN.
(1)求证:BM=MN;
(2)∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.
参考答案:
【答案】
(1)
证明:在△CAD中,∵M、N分别是AC、CD的中点,
∴MN∥AD,MN= ![]() AD,
AD,
在RT△ABC中,∵M是AC中点,
∴BM= ![]() AC,
AC,
∵AC=AD,
∴MN=BM
(2)
解:∵∠BAD=60°,AC平分∠BAD,
∴∠BAC=∠DAC=30°,
由(1)可知,BM= ![]() AC=AM=MC,
AC=AM=MC,
∴∠BMC=∠BAM+∠ABM=2∠BAM=60°,
∵MN∥AD,
∴∠NMC=∠DAC=30°,
∴∠BMN=∠BMC+∠NMC=90°,
∴BN2=BM2+MN2,
由(1)可知MN=BM= ![]() AC=1,
AC=1,
∴BN= ![]()
【解析】(1)根据三角形中位线定理得MN= ![]() AD,根据直角三角形斜边中线定理得BM=
AD,根据直角三角形斜边中线定理得BM= ![]() AC,由此即可证明.(2)首先证明∠BMN=90°,根据BN2=BM2+MN2即可解决问题.
AC,由此即可证明.(2)首先证明∠BMN=90°,根据BN2=BM2+MN2即可解决问题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形的一个外角为α,且该多边形的内角和与α的和等于840°,则这个多边形的边数为_____,α=_____度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若等腰三角形的周长为10cm,其中一边长为2cm,则该等腰三角形的底边长为____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线AB平移至△FEG,DE、FG相交于点H.

(1)判断线段DE、FG的位置关系,并说明理由;
(2)连结CG,求证:四边形CBEG是正方形. -
科目: 来源: 题型:
查看答案和解析>>【题目】若一元二次方程x2+2x+m+1=0有实数根,则( )
A.m的最小值是1
B.m的最小值是﹣1
C.m的最大值是0
D.m的最大值是2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图一:在Rt△ABC中,∠C=90°AD、BE分别是△ABC中∠A、∠B的平分线,AD、BE交于点F,过F点做FH⊥AD交AC于点H,易证:AH+DB=AB;
(1)若将Rt△ABC中∠BAC、∠ABC的内角平分线改成外角平分线,即:AF、BF分别是∠BAC、∠ABC的外角平分线交于F点,FH⊥AF交直线AC于H点,如图二:请写出线段AH、BD、AB之间的数量关系,并证明。
(2)若将Rt△ABC中∠BAC、∠ABC的内角平分线改成一个是外角平分线,即:AF是∠A的内角平分线,BE是∠B的外角平分线交于F点,FH⊥AD交AC于点H.如图三:请写出线段AH、BD、AB之间的数量关系,无需证明。

-
科目: 来源: 题型:
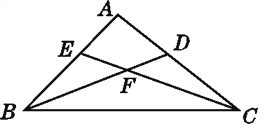
查看答案和解析>>【题目】如图,以CD为公共边的三角形是____________;∠EFB是____________的内角;在△BCE中,BE所对的角是____________,∠CBE所对的边是____________;以∠A为公共角的三角形是____________.
相关试题

