【题目】已知:抛物线y=x2+4x+4+m的图像与y轴交于点C,点B与点C的纵坐标相同,一次函数y=kx+b的与二次函数交于A、B两点,且A点坐标为(-1,0).
(1)求二次函数与一次函数的解析式;
(2)若抛物线对称轴上存在一点P,直线PC将△ABC分成面积为1:2两部分,求P点坐标。

参考答案:
【答案】(1)二次函数的解析式为y=x2+4x+3 ,一次函数的解析式为:y=-x-1;(2) P1(-2,1 ),P2(-2, ![]() ).
).
【解析】解:(1)因为A(-1,0)在抛物线y=x2+4x+4+m上
![]() =-1
=-1
所以二次函数的解析式为y=x2+4x+3
所以B点的坐标为(-4,3)
设BA的解析式为y=kx+b过A(-1,0),B (-4,-3)点
![]() 得 -k+b=0
得 -k+b=0
-4k+b=3
得k=-1 b=-1
BA的解析式为:y=-x-1
(2) P1(-2,1 ) P2(-2, ![]() )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图一:在Rt△ABC中,∠C=90°AD、BE分别是△ABC中∠A、∠B的平分线,AD、BE交于点F,过F点做FH⊥AD交AC于点H,易证:AH+DB=AB;
(1)若将Rt△ABC中∠BAC、∠ABC的内角平分线改成外角平分线,即:AF、BF分别是∠BAC、∠ABC的外角平分线交于F点,FH⊥AF交直线AC于H点,如图二:请写出线段AH、BD、AB之间的数量关系,并证明。
(2)若将Rt△ABC中∠BAC、∠ABC的内角平分线改成一个是外角平分线,即:AF是∠A的内角平分线,BE是∠B的外角平分线交于F点,FH⊥AD交AC于点H.如图三:请写出线段AH、BD、AB之间的数量关系,无需证明。

-
科目: 来源: 题型:
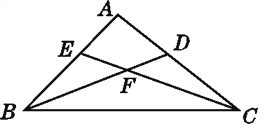
查看答案和解析>>【题目】如图,以CD为公共边的三角形是____________;∠EFB是____________的内角;在△BCE中,BE所对的角是____________,∠CBE所对的边是____________;以∠A为公共角的三角形是____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.a3a2=a6B.(ab3)2=a2b6
C.(a﹣b)2=a2﹣b2D.5a﹣3a=2
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知三角形的三边长都是整数,最长边长为8,则满足上述条件的互不全等的三角形的个数为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 相等的角是对顶角B. 同位角相等
C. 两直线平行,同旁内角相等D. 垂线段最短
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.易证:CE=CF.
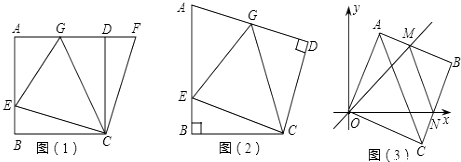
(1)在图1中,若G在AD上,且∠GCE=45°.试猜想GE,BE,GD三线段之间的数量关系,并证明你的结论.
(2)运用(1)中解答所积累的经验和知识,完成下面两题:
①如图2,在四边形ABCD中∠B=∠D=90°,BC=CD,点E,点G分别是AB边,AD边上的动点.若∠BCD=α,∠ECG=β,试探索当α和β满足什么关系时,图1中GE,BE,GD三线段之间的关系仍然成立,并说明理由.
②在平面直角坐标中,边长为1的正方形OABC的两顶点A,C分别在y轴、x轴的正半轴上,点O在原点.现将正方形OABC绕O点顺时针旋转,当A点第一次落在直线y=x上时停止旋转,旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N(如图3).设△MBN的周长为p,在旋转正方形OABC的过程中,p值是否有变化?若不变,请直接写出结论.
相关试题

